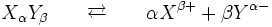Produit de solubilité - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le produit de solubilité est la constante d'équilibre correspondant à la dissolution d'un solide dans un solvant.
Définition
Soit par exemple la dissolution du solide ionique de formule XαYβ
La dissolution est décrit par la réaction suivante :
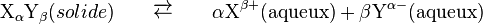
En utilisant la loi d'action de masse on obtient la formule :
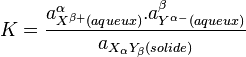
Le composé ionique étant un solide pur son activité est égale à 1. Les activités des ions dans un milieu aqueux s'assimilent à leurs concentrations en mole par litre (mol/l).
Le produit de solubilité est :
![K_s = \left[ X^{\beta+} \right] ^{\alpha} . \left[ Y^{\alpha-} \right] ^{\beta}](https://static.techno-science.net/illustration/Definitions/autres/9/9ae67384ed649e2629a7833b48415ed4_9a480219c26094bc96b69dca5dc52e60.png)

Si le produit des concentrations ( [X+].[Y-] ) des deux ions constitutifs du composé ionique reste inférieur à Ks, le composé ionique se dissocie entièrement.
Si le produit [X+].[Y-] est atteint, la solution est saturée et l'addition de composé ionique se traduit par un précipité. Une addition supplémentaire du composé XY, ne modifie pas la concentration en ions mais augmente la quantité de précipité.
Relation entre le produit de solubilité et la solubilité
| |
Exemple d'un composé ionique de type XY
Le bromure de cuivre se dissout dans l'eau suivant léquilibre suivant :

Soit s la solubilité du bromure de cuivre. La dissolution de s mole par litre de CuBr donne s mole par litre de Cu+ et s mole par litre de Br-. On peut décrire la situation de la manière suivante :
|
| |||
| Espèce chimique | CuBr | Cu+ | Br- |
|---|---|---|---|
| t=0 | s | 0 | 0 |
| Équilibre | 0 | s | s |
Le produit de solubilité du bromure de cuivre s'écrit :
![K_s = \left[ Cu^+ \right] . \left[ Br^- \right] = 5,3 . 10^{-9}](https://static.techno-science.net/illustration/Definitions/autres/b/b5d465d65e13c9c220facabaa6a57520_b9c59ef4e51f7102188e5f66511ecc47.png)
Avertissement : une constante d'équilibre étant sans dimension, il convient en toute rigueur de l'équilibrer en la multipliant ou la divisant autant que nécessaire par la concentration standard C0 = 1mol.L − 1 soit :
![K_s = \frac{\left[ Cu^+ \right] . \left[ Br^- \right]}{{C^0}^2} = 5,3 . 10^{-9}](https://static.techno-science.net/illustration/Definitions/autres/3/3cad1e861212f8a9c17b8aa26e6dea64_8051e6176cf706d17eabf4339fad2124.png)
On néglige en général ce terme en C° pour conserver la première écriture, même si l'équation aux dimensions est fausse.
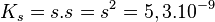
donc
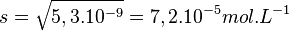
La masse molaire du bromure de cuivre est
MCuBr = 63,55 + 79,90 = 143,45g.mol − 1,
La solubilité massique du bromure de cuivre est
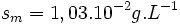
Exemple d'un composé ionique de type X2Y
Le carbonate d'argent se dissout suivant l'équilibre :

Soit s la solubilité du carbonate d'argent. La dissolution de s mole de AgCO3 donne 2s mole de Ag+ et s mole de CO3-. On peut décrire la situation de la manière suivante :
|
| |||
| Espèce chimique | Ag2CO3 | Ag+ | CO32- |
|---|---|---|---|
| t=0 | s | 0 | 0 |
| Équilibre | 0 | 2s | s |
![K_s = \left[ Ag^+ \right]^2 . \left[ CO_3^{2-} \right] = 8,1.10^{-18}](https://static.techno-science.net/illustration/Definitions/autres/0/08edb33b7ee2b674d752523d4160fad4_7c2131363e09c0d5707455061bf363ee.png)
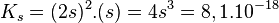
![s = \sqrt[3]{8,1.10^{-18}/4}](https://static.techno-science.net/illustration/Definitions/autres/7/72affc1aa40658eda885783098341d64_2fa711b444184db401791e14cfc716e5.png)
donc
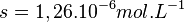
La masse molaire du carbonate d'argent est
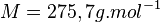
La solubilité massique du carbonate d'argent est
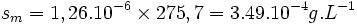
Généralisation
Soit la dissolution d'un composé ionique de formule générale XαYβ
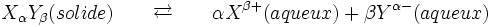
Soit s la solubilité de XαYβ. La dissolution de s mole de XαYβ donne α s mole de Xα et β s mole de Yβ.. On peut décrire la situation de la manière suivante :
|
| |||
| Espèce chimique | XαYβ | Xβ+ | Yα- |
|---|---|---|---|
| t=0 | s | 0 | 0 |
| Équilibre | 0 | αs | βs |
![K_s = \left[ X^{\beta+} \right]^{\alpha} . \left[ Y^{\alpha-} \right]^{\beta}](https://static.techno-science.net/illustration/Definitions/autres/9/9ae67384ed649e2629a7833b48415ed4_9a480219c26094bc96b69dca5dc52e60.png)
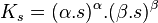
La relation générale entre le K_s et la solubilité est la suivante :
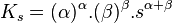
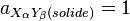
![a_{X^{\beta+} (aqueux)}^{\alpha} = \left[ X^{\beta+} \right] ^{\alpha}](https://static.techno-science.net/illustration/Definitions/autres/5/53f84df4672e9f5ccbc5acada51f1e0d_41ac36878c8a4b80b7cc7fa0ea039ec8.png)
![a_{Y^{\alpha-} (aqueux)}^{\beta} = \left[ Y^{\alpha-} \right] ^{\beta}](https://static.techno-science.net/illustration/Definitions/autres/8/849ee04092d168e5dce9c50ad6b0aa52_7c9c8fc39876a1240064c2b7fd24f10f.png)