Groupe de Janko - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, les groupes de Janko J1, J2, J3 et J4 sont quatre des vingt-six groupes sporadiques; leurs ordres respectifs sont :
|
|
|
|
|
|
|
|
|
|
|
|
J1
Le plus petit groupe de Janko,
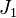
-
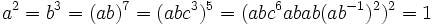
Janko trouva une représentation modulaire en termes de matrices orthogonales 7 x 7 dans le corps à 11 éléments, avec les générateurs donnés par
et
-

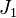
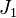
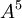
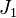
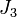
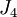
J3
Le troisième groupe de Janko, aussi connu comme le groupe de Higman-Janko-McKay, est un groupe sporadique fini simple d'ordre 50 232 960. L'évidence de son existence a été découverte par Janko et a été montré par Higman et McKay. En termes de générateurs a, b, c, et d, son groupe d'automorphisme
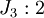
![a^{17} = b^8 = a^ba^{-2} = c^2 = b^cb^3 = (abc)^4 = (ac)^{17} = d^2 = [d, a] = [d, b] = (a^3b^{-3}cd)^5 = 1\,](https://static.techno-science.net/illustration/Definitions/autres/3/302509eb1206ae81dfcc927af9ac17b8_2a9401336c374ff376f544bed5062111.png)
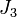
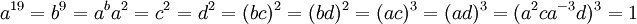
J2
Le deuxième groupe de Janko, d'ordre 604 800 possède une présentation en termes de deux générateurs a et b : en termes desquels il a un automorphisme extérieur envoyant b vers b2. Le groupe est aussi appelé le groupe de Hall-Janko ou le groupe de Hall-Janko-Wales, puisqu'il a été prévu par Janko et construit par Hall et Wales. C'est un sous-groupe d'index deux du groupe des automorphismes du graphe de Hall-Janko, conduisant à une représentation de permutation de degré 100. Cette représentation possède un stabilisateur à un point avec les orbites de 36 et 63, isomorphe au groupe unitaire
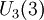
Nous pouvons aussi l'exprimer en termes d'une représentation modulaire à 6 dimensions sur le corps à 4 éléments; si en caractéristique deux, nous avons
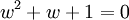
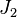
et
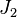
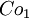
Griess relate [p. 123] comment Marshall Hall, en tant qu'éditeur de The Journal of Algebra, reçut un court article intitulé "Un groupe simple d'ordre 604 801." Oui, 604 801 est premier.
J4
Le quatrième groupe de Janko a été montré comme probable Janko en 1976, puis son existence unique fut démontrée par Simon Norton en 1980. C'est un groupe fini simple unique d'ordre
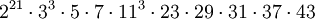
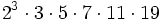
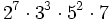
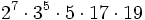
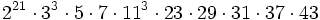

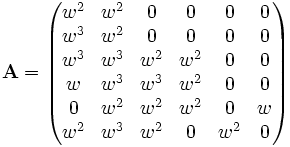
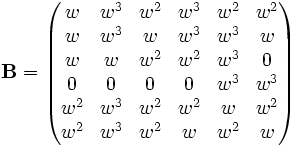
![a^2=b^3=c^2=(ab)^{23}=[a,b]^{12}=[a,bab]^5=[c,a]=\,](https://static.techno-science.net/illustration/Definitions/autres/0/0507d15f39193506e8b32d32061aa970_f121c7d304830da602965a67a3be871c.png)
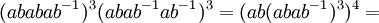
![[c,bab(ab^{-1})^2(ab)^3]=(bc^{bab^{-1}abab^{-1}a})^3=\,](https://static.techno-science.net/illustration/Definitions/autres/5/5595a92a13da320ea94c2d857f06978b_d34728821731f83b7323fcd90da06b37.png)