Homotopie - Définition
La liste des auteurs de cet article est disponible ici.
Introduction

L'homotopie est une notion de topologie algébrique. Elle formalise la notion de déformation continue d'un objet à un autre. Deux lacets sont dit homotopes lorsqu'il est possible de passer continument de l'un à l'autre, comme illustré sur la figure de droite. Ce concept se généralise à bien d'autres objets que des lacets. Ainsi, les fonctions définissant les deux jeux de lettres de droite (les bleues et les rouges) sont aussi homotopiques.
L'homotopie fournit des informations sur la nature topologique d'un espace. Une bande circulaire d'un plan ne peut être équivalente, au sens de l'homéomorphisme, à un disque. Dans un disque, tout lacet est homotope à un point. Dans une bande circulaire, ce n'est pas le cas. Cette remarque est source de démonstrations, comme celle du théorème de d'Alembert-Gauss, du point fixe de Brouwer, de Borsuk-Ulam ou encore celle du théorème du sandwich au jambon, qui précise que quels que soient deux solides mesurables et bornés d'un espace euclidien de dimension trois, il existe un hyperplan qui sépare chacun des solides en deux parties de mesures égales.
Définition
Homotopie entre deux chemins
Soit X un espace topologique. Un chemin continu de X est une application continue du segment réel [0, 1] dans X. Cette définition correspond à l'idée intuitive de chemin, au sens de sentier qui part d'un point pour arriver à un autre.
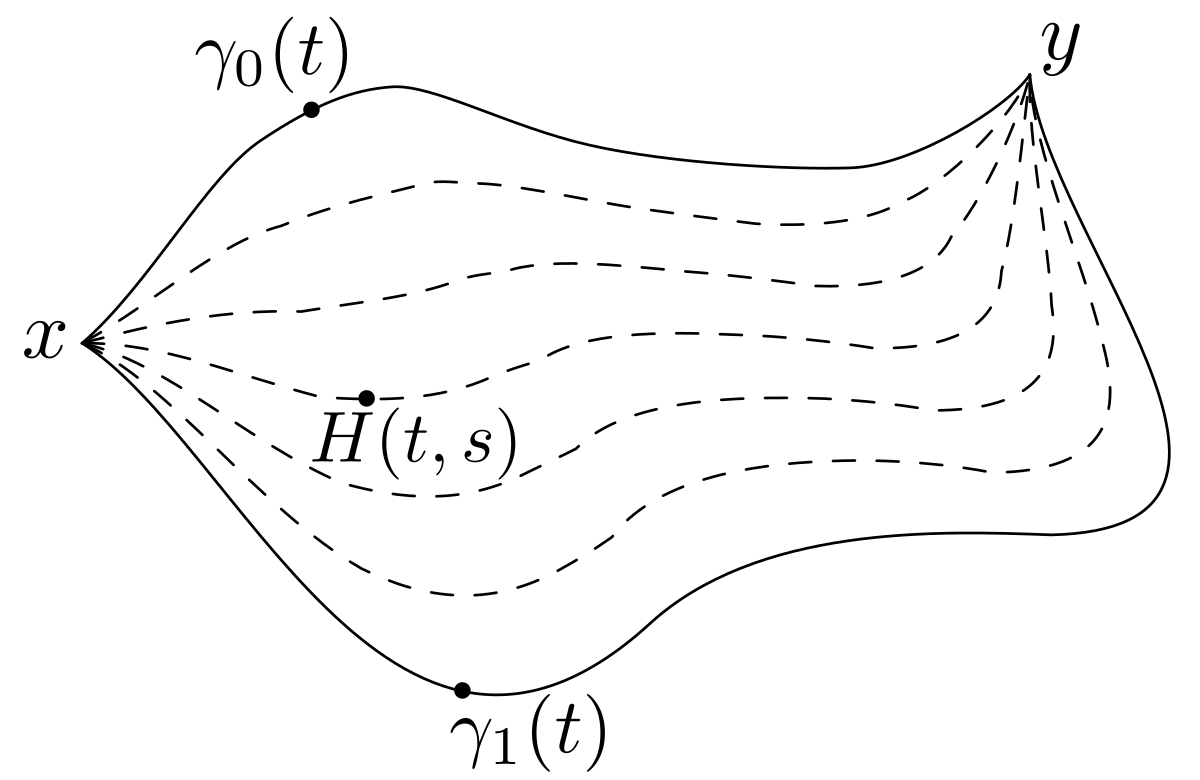
- Deux chemins continus γ0 et γ1 de X sont dits homotopes lorsqu'il existe une application continue H de [0, 1]2 dans X tel que l'application qui à t associe H(t, 0) est égale à γ0 et celle qui à t associe H(t, 1) est égale à γ1 .
![\forall t \in [0,1]\quad H(t,0) = \gamma_0(t)\text{ et } H(t,1) = \gamma_1(t)](https://static.techno-science.net/illustration/Definitions/autres/f/f384a79d6e74ad88f064317652cb47e7_da019e111efa932e7d36af76c2df6a4b.png)
Cette situation ne décrit pas encore exactement la situation représentée à droite. Sur l'illustration, les deux chemins γ0 et γ1 possèdent la même origine x ainsi que la même extrémité y. C'est-à-dire :
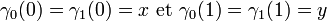
- Deux chemins continus γ0 et γ1 de X ayant même origine et même extrémité, sont dits homotopes strictement lorsqu'ils sont homotopes d'homotopie H et que, pour tout s élément de [0, 1] on dispose des égalités H(0, s) = x et H(1, s) = y.
![\forall s \in [0,1]\quad H(0,s) = x\text{ et } H(1,s) = y](https://static.techno-science.net/illustration/Definitions/autres/3/30947dcb87346f70ef81f5e0d921187f_057b543e81e152a9db7e3d236420fa33.png)
Homotopie entre deux fonctions
Les définitions précédentes se généralisent à deux fonctions continues f et g d'un espace topologique X dans un espace topologique Y.
- Les deux fonctions f et g sont dites homotopes, d'homotopie H, si H est une fonction continue de X × [0, 1] dans Y tel que l'application qui à t associe H(t, 0) est égale à f et celle qui à t associe H(t, 1) est égale à g.
Il est possible de généraliser la deuxième définition. Soit A un sous-ensemble de X tel que les restrictions de f et de g à A soient égales.
- Les deux fonctions f et g sont dites homotopes relativement à A si f et g sont homotopes, d'homotopie H et que :
![\forall s \in [0,1],\; \forall a \in A \quad H(a,s) = f(a) = g(a)](https://static.techno-science.net/illustration/Definitions/autres/8/8d911706fbe7dddf95cc17bcf8f676c6_c9c941ff12c8721509a1d6b71f4db002.png)
Usages
Théorème de d'Alembert-Gauss
L'homotopie est source de nombreuses démonstrations. Un exemple célèbre est celui du théorème de d'Alembert-Gauss qui indique que tout polynôme à coefficients complexes et non constant admet au moins une racine dans C.
Pour le démontrer, on considère un polynôme unitaire p(z) n'ayant aucune racine dans C et on note n son degré. Pour chaque réel positif r, on définit le lacet αr par :
![\forall t \in [0,1]\quad \alpha_r(t) = \frac {p(r\exp(2\pi i \cdot t))/p(r)}{|p(r\exp(2\pi i \cdot t))/p(r)|}](https://static.techno-science.net/illustration/Definitions/autres/b/b13270a1dc56bd6238ae8a861fcc5cf2_cefc4d175fad1f48e867f1864ea0a541.png)
Par définition, αr est un lacet défini sur le cercle. Si r est égal à 0, on obtient le lacet constant égal à 1. Comme la fonction, qui à r et t associe αr(t) est continue, tous les lacets αr sont homotopes à un point.
Soit (aj) la suite presque nulle des coefficients de p et ρ un nombre réel plus grand que 1 et que Σ|aj| la somme des valeurs absolues des coefficients de p. Si z est un nombre complexe de module égal à ρ :

On définit le polynôme ps(z) et le lacet βs par :
![p_s(z) = s(a_0 + a_1z + \cdots + a_{n-1}z^{n-1}) + z^n,\quad \forall t \in [0,1]\quad \beta_s(t) = \frac {p_s(\rho\exp(2\pi i \cdot t))/p_s(\rho)}{|p_s(\rho\exp(2\pi i \cdot t))/p_s(\rho)|}](https://static.techno-science.net/illustration/Definitions/autres/0/06a4ce8d365deb18adb2b221eacd1e9c_07b2d053b511e3435ac61d4301d2b734.png)
La majoration (1) montre que le polynôme ps n'admet pas de racine de module ρ et le lacet βs est bien défini. Si s est égal à 0, le lacet β0 fait n tours autour de l'origine, d'après le paragraphe précédent. Comme la fonction si à s et t associe βs(t) est continue, le lacet β1 est homotope à β0. Or le lacet β1 est égal au lacet αρ. Comme le lacet αρ est homotope à un point c'est-à-dire qu'il fait 0 tour autour de l'origine, n est égal à 0. Autrement dit, les seuls éventuels polynômes n'ayant pas de racine dans C sont les polynômes constants.
Groupe fondamental
Si X est un espace topologique, on peut composer deux lacets de même base p (c'est-à-dire de même origine et même extrémité p) α1 et α2 en construisant un lacet parcourant d'abord la trajectoire de α1, puis celle de α2. Cette composition est compatible avec la relation d'équivalence est homotope à. Quotienté par cette relation d'équivalence, on obtient une structure de groupe appelé groupe fondamental ou groupe de Poincaré. Cette notion se généralise et permet de définir une infinité de groupes d'homotopie.
Ce groupe est à l'origine de démonstrations. L'une des plus célèbres est celle du théorème du point fixe de Brouwer en dimension deux, qui indique que toute application continue du disque dans lui-même admet un point fixe.
Topologie algébrique
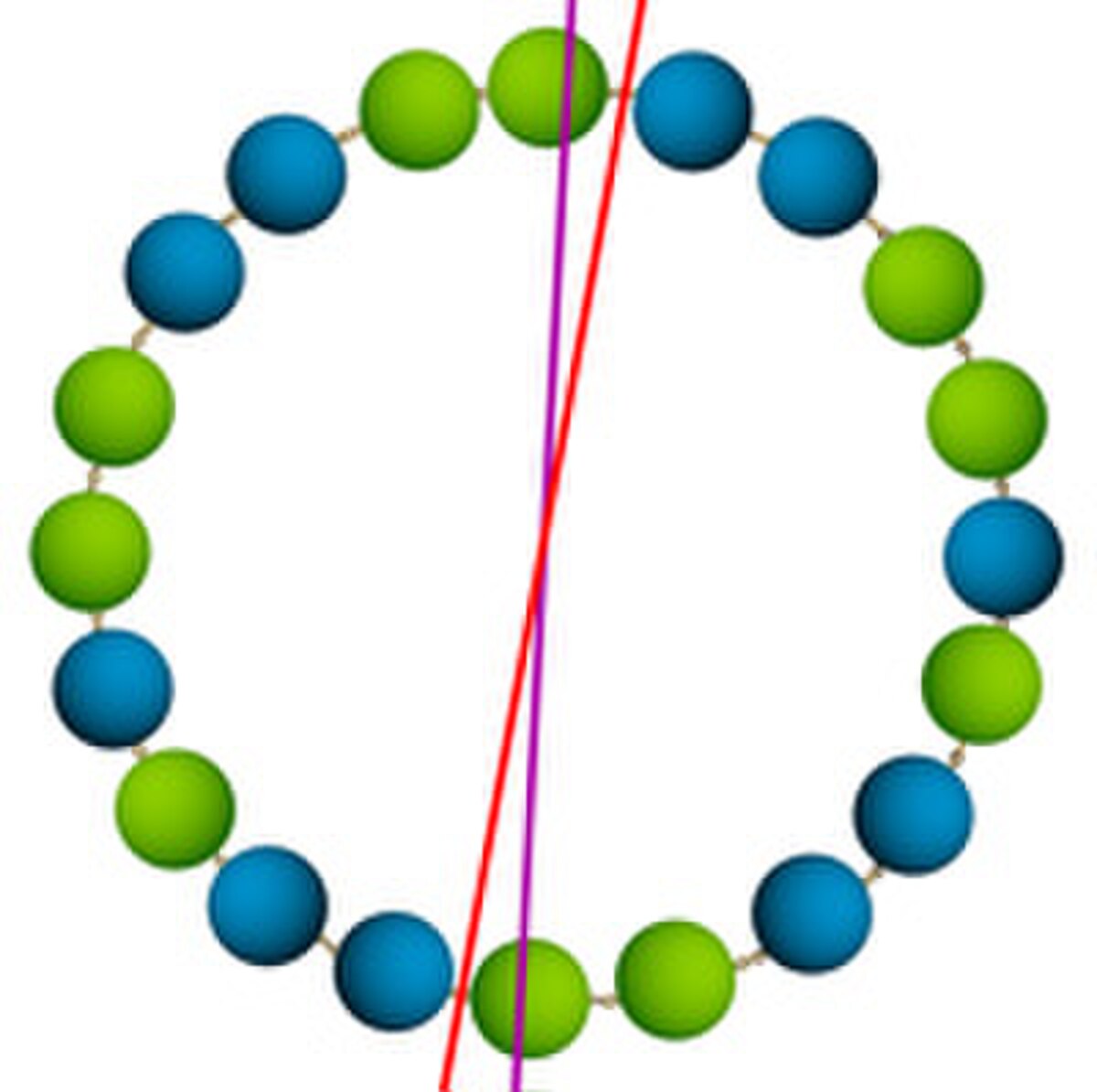
L'homotopie est l'un des outils essentiels de la topologie algébrique. Le cas le plus simple, celui des lacets est la source de nombreuses démonstrations dans ce domaine. En plus du théorème de d'Alembert-Gauss ou de celui du point fixe de Brouwer, celui de Borsuk-Ulam est caractéristique d'une démarche de la topologie algébrique. En dimension deux, il indique que toute application continue de la sphère dans R2 admet deux points antipodaux de même image. Autrement dit, il existe toujours sur terre deux points situés aux antipodes ayant exactement la même température et la même pression. Il permet de résoudre par l'affirmative quelques questions célèbres comme celle du sandwich au jambon : Existe-il un plan qui coupe trois solides bornés et mesurables (correspondant à deux tartines de pain et une tranche de jambon) en deux parties de volumes égaux pour les trois solides. Les raisonnements de topologie algébrique faisant usage de l'homotopie permettent aussi de démontrer que si trois fermés ont pour union la sphère, l'un d'entre eux au moins contient deux points antipodaux. On peut citer encore la question du partage du collier et des deux voleurs : un collier, illustré à gauche, est formé de deux types de perles différentes, chaque type contient un nombre de perles paire. Une fois encore, l'homotopie permet de montrer qu'il est possible de couper le colliers en deux coups de ciseaux tel que chaque côté contient le même nombre de perles pour chacun des deux types. Elle permet de trouver l'axe de coupe violet, une petite rotation permet de passer à l'axe de coupe rouge, qui garde intact les perles.