Groupe alterné - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, et plus précisément en théorie des groupes, le groupe alterné de degré n, souvent noté An, est un sous-groupe distingué du groupe symétrique des permutations d'un ensemble fini à n éléments. Ce sous-groupe est composé des éléments produits d'un nombre pair de transpositions. Une transposition est une permutation φ réduite à l'identité sauf sur exactement 2 éléments a et b. Cette propriété implique que φ(a) = b et φ(b) = a.
Il existe un groupe alterné pour chaque groupe symétrique, donc pour chaque entier n supérieur ou égal à 2 et il se note habituellement An, parfois avec un «
Le groupe alterné est la structure source de certains casse-tête mathématique comme le jeu de taquin ou le cube de Rubik. Les mouvements possibles dans les deux jeux cités sont des éléments d'un groupe alterné. Cette propriété permet de montrer qu'il n'est pas possible de permuter deux cases du taquin sans modifier le reste du jeu.
Les groupes alternés de degré 4 et 5 se représentent comme le groupe des rotations laissant invariant un polyèdre régulier, le tétraèdre pour A4 et le dodécaèdre ou encore l'icosaèdre pour A5.
Construction du groupe
Définition
Un résultat, à la base de la définition de la signature, stipule que le nombre de transpositions nécessaire pour décomposer une permutation donnée est toujours de même parité. Ainsi, le cycle (abc), qui transforme a en b, b en c et c en a peut se décomposer en deux transpositions (ab), puis (bc) ou encore en (ac) puis (bc) mais jamais en un produit d'un nombre impair de transpositions.
Définition — Une permutation est dite paire lorsqu'elle se décompose en un nombre pair de transpositions. Dans le cas inverse, la permutation est dite impaire.
Cette définition est à l'origine de celle d'un groupe alterné.
Définition — Le groupe alterné de degré n, noté An, est le sous-groupe des permutations paires de degré n.
Remarque : On trouve aussi l'expression groupe alterné d'indice n, à la place de groupe alterné de degré n. Ce choix est un peu ambigu, l'indice de An dans Sn désigne, pour d'autres auteurs, l'ordre du groupe quotient Sn/An. On trouve encore le terme d'ordre pour décrire le degré. Cette convention est plus rarement utilisée, en effet le terme d'ordre est utilisé en théorie des groupes pour décrire le cardinal d'un groupe, ce choix introduit une confusion parfois regrettable.
Propriétés élémentaires
Dans toute la suite de l'article, n désigne un entier supérieur ou égal à 2. La définition précédente repose sur une propriété fondamentale partagée par toutes les permutations :
Propriété 1 — La parité du nombre de transposition nécessaire pour décomposer une permutation donnée est indépendante de la décomposition choisie.
Cette propriété se démontre à l'aide du concept de signature d'une permutation, traitée dans le paragraphe suivant. Une fois établie, une deuxième propriété se démontre simplement :
Propriété 2 — L'ensemble An des permutations paires de Sn forme un sous-groupe distingué.
En effet, An est non vide car il contient l'élément neutre, qui se décompose en zéro transposition, ou encore en deux fois la même transposition. Si φ1 et φ2 sont deux permutations paires alors leur produit est aussi une permutation paire. Pour s'en rendre compte, il suffit de remarquer que φ1 et φ2 correspondent à des produits de transpositions en nombres pairs. Ainsi il existe des transpositions σ1, ..., σ2p, τ1, ..., τ2q, tel que φ1 = σ1...σ2p et φ2 = τ1...τ2q. Le produit φ1.φ2 est égal à σ1...σ2p.τ1...τ2q. Comme la somme de 2 nombres pairs est paire le produit est bien une permutation paire. Il reste à montrer que l'inverse de φ1 est bien une permutation paire, cet inverse est égal à σ2p...σ1, le produit des mêmes transpositions pris dans l'ordre inverse.
Dire que An est distingué revient à dire que si φ est élément du sous-groupe et si σ est une permutation quelconque de Sn, alors σ.φ.σ-1 est une permutation paire. En effet, σ est le produit d'un nombre pair de transpositions, et le paragraphe précédent montre que σ-1 se décompose en autant de transpositions que σ. La somme du nombre de toutes ces transpositions est nécessairement paire.
Propriété 3 — L'ordre de An est la moitié de celui de Sn, c'est-à-dire n!/2.
En effet, considérons l'application f de Sn dans Sn qui, à une permutation φ, associe φσ. Ici σ désigne une transposition de Sn. Une telle application est, dans un groupe, appelé translation à droite. La fonction f, comme toute translation, est une bijection. L'image de An est incluse dans l'ensemble des permutations impaires. La bijection de f montre que l'ordre de An est plus petit que le cardinal de l'ensemble des permutations impaires. De même l'image par f d'une permutation impaire est paire, la bijection de f montre aussi que le cardinal de l'ensemble des permutations impaires est plus petit que celui des permutations paire, c'est-à-dire l'ordre de An. Il y a égalité entre l'ordre de An et le cardinal de l'ensemble des permutations impaires. Ces deux ensembles forment une partition de Sn de 2 sous-ensembles de même cardinal, ce qui termine la démonstration.
Propriété 4 — Soit m, un entier plus petit que n. Un cycle de Sn et de longueur m est élément du groupe alterné si, et seulement si, m est impair.
Une petite récurrence vient à bout de la démonstration de cette propriété. Si n est égal à 2, comme une transposition est impaire, la propriété est vérifiée. Supposons la propriété vraie à l'ordre m - 1 et étudions la parité d'un cycle le longueur m, noté (a1...am-1am). On remarque que le cycle est produit de la transposition (am-1am) et du cycle (a1...am-1). L'hypothèse de récurrence montre que le cycle de longueur m une permutation paire si et seulement si m - 1 est paire, ce qui termine la démonstration.
Signature
La signature d'une permutation est la parité du nombre d'inversions contenues dans une permutation. On démontre que cette application est un morphisme de groupe de Sn dans {-1, 1} et que la signature d'une transposition est toujours égale à -1. On en déduit que le nombre de transpositions nécessaire pour décomposer une permutation ne peut à la fois être paire et impaire, sinon la signature ne serait pas un morphisme de groupe. En effet, si φ est une permutation qui se décompose en p ou bien q transpositions, la signature de φ, d'après la propriété de morphisme est à la fois égale à (-1)p et (-1)q, ce qui montre que p et q sont de même parité. On en déduit une nouvelle définition du groupe alterné, équivalente à la précédente :
Définition alternative — Le groupe alterné An est le noyau du morphisme signature du groupe symétrique Sn.
Cette approche offre des démonstrations alternatives aux propositions du paragraphe précédent numérotées de 2 et 3. Le noyau d'un morphisme est toujours un sous-groupe distingué, ce qui montre que An est un sous-groupe distingué. L'ordre du noyau que multiple l'ordre de l'image d'un morphisme de groupe est égal à l'ordre du groupe de départ, ce qui permet de déterminer l'ordre du groupe alterné.
Exemples
Le groupe alterné de degré 2 ne contient que l'élément neutre.
Le groupe symétrique de degré 3 est d'ordre 6 et contient : l'identité, trois transpositions et deux cycles d'ordre 3. Le groupe alterné de degré 3 ne comporte que l'identité et les cycles d'ordre 3 :
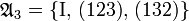
Comme tout groupe contenant 3 éléments, il est isomorphe au groupe cyclique d'ordre 3.
Le groupe symétrique de degré 4 est d'ordre 24, le groupe alterné associé est d'ordre 12. Il contient les cycles d'ordre 3 et les produits de 2 cycles d'ordre 2 de supports disjoints :
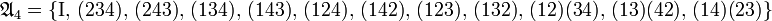
Le groupe symétrique de degré 4 n'est pas abélien. Pour s'en rendre compte, il suffit de remarquer que les transpositions (12) et (23) ne commutent pas. Le produit des deux dans les deux ordres donnent les deux cycles de support 1, 2 et 3. Aucun groupe alterné de degré supérieur à 4 n'est abélien, en effet ces groupes contiennent tous une copie de A4, qui ne l'est pas. Ce groupe est néanmoins résoluble, il contient un sous-groupe distingué abélien, composé des produits de deux transpositions à support disjoints et de l'élément neutre. Ce groupe est abélien car isomorphe au groupe de Klein et le quotient de A4 par le groupe distingué est aussi abélien car d'ordre 3 et donc cyclique.
Le groupe symétrique de degré 5 est d'ordre 60. Il est étudié plus avant à la suite de cet article.
Jeu de taquin
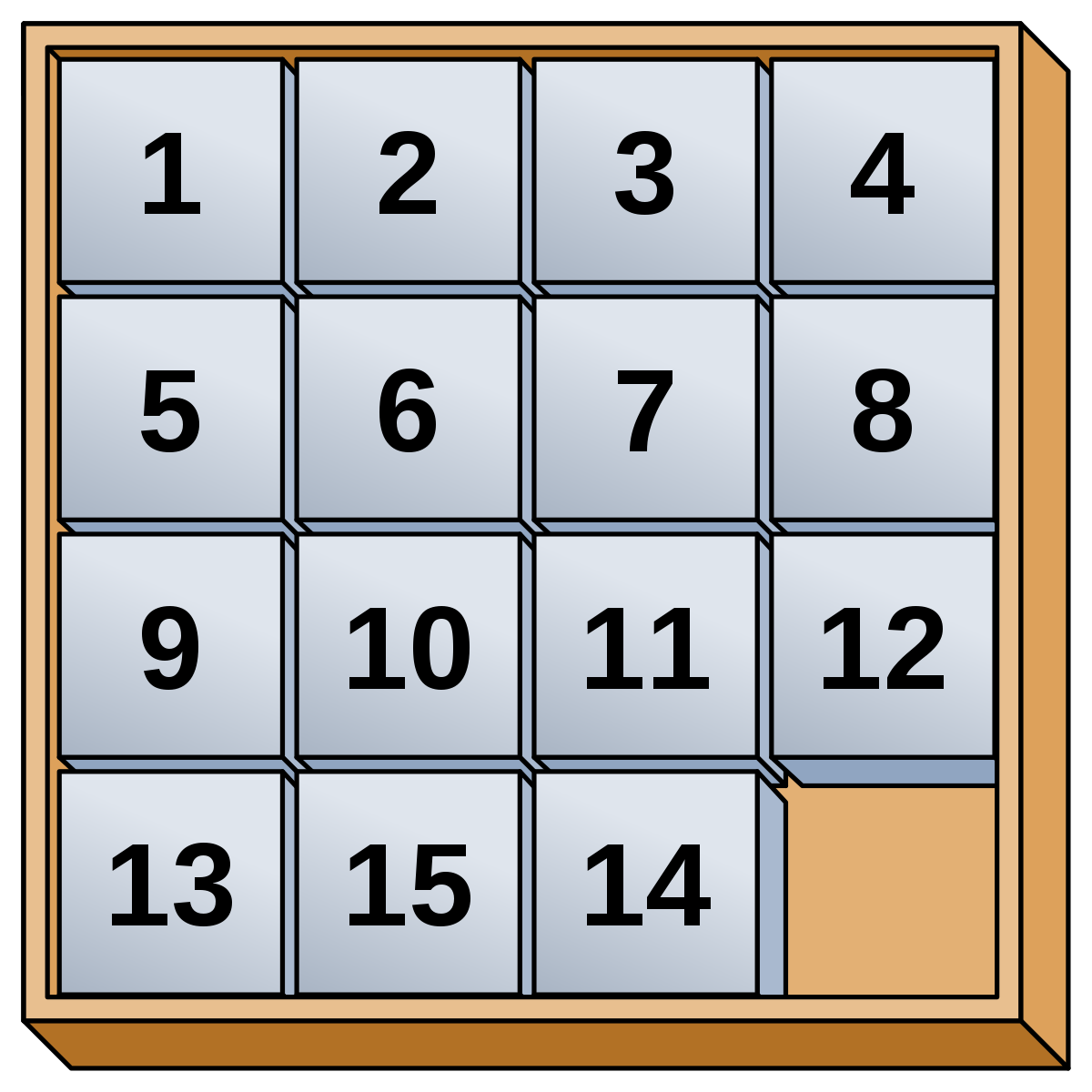
Le jeu de taquin, est un jeu solitaire qui se présente sous la forme d'un damier composé de 15 cases et d'une 16ième manquante. Sa théorisation mathématique date de 1879 et se fonde sur les propriétés du groupe alterné. Une des questions posée par Sam Loyd est celle de la résolution du jeu de taquin illustré à droite. Elle correspond à la résolution d'un état du jeu où toutes les cases sont à la bonne position exceptées celles numérotées 14 et 15, qui sont interverties. Elle est impossible si l'on impose à la case vide d'être en bas à droite. Elle l'est si on admet que la case vide soit en haut à gauche et que la première ligne ne contienne que les cases 1, 2 et 3.
Si l'on considère un mouvement comme une permutation des cases numérotées de 1 à 15, alors le groupe des permutations de degré 15 opère sur le jeu de taquin. Pour être plus précis, le groupe qui opère est un sous-groupe engendré par les différentes permutations possibles. Il est relativement simple de vérifier que les permutations engendrant le sous-groupe sont toutes des cycles d'ordre 3 ou 5. Ces permutations sont toutes dans le groupe alterné A15. Le groupe qui opère sur le jeu de taquin est un sous-groupe du groupe alterné A15, qui ne contient aucune transposition. C'est une manière simple de démontrer que la configuration de droite n'est pas résoluble.
D'autres solitaires, comme l'Âne rouge ou le Rubik's cube utilisent de manière analogue le groupe alterné.
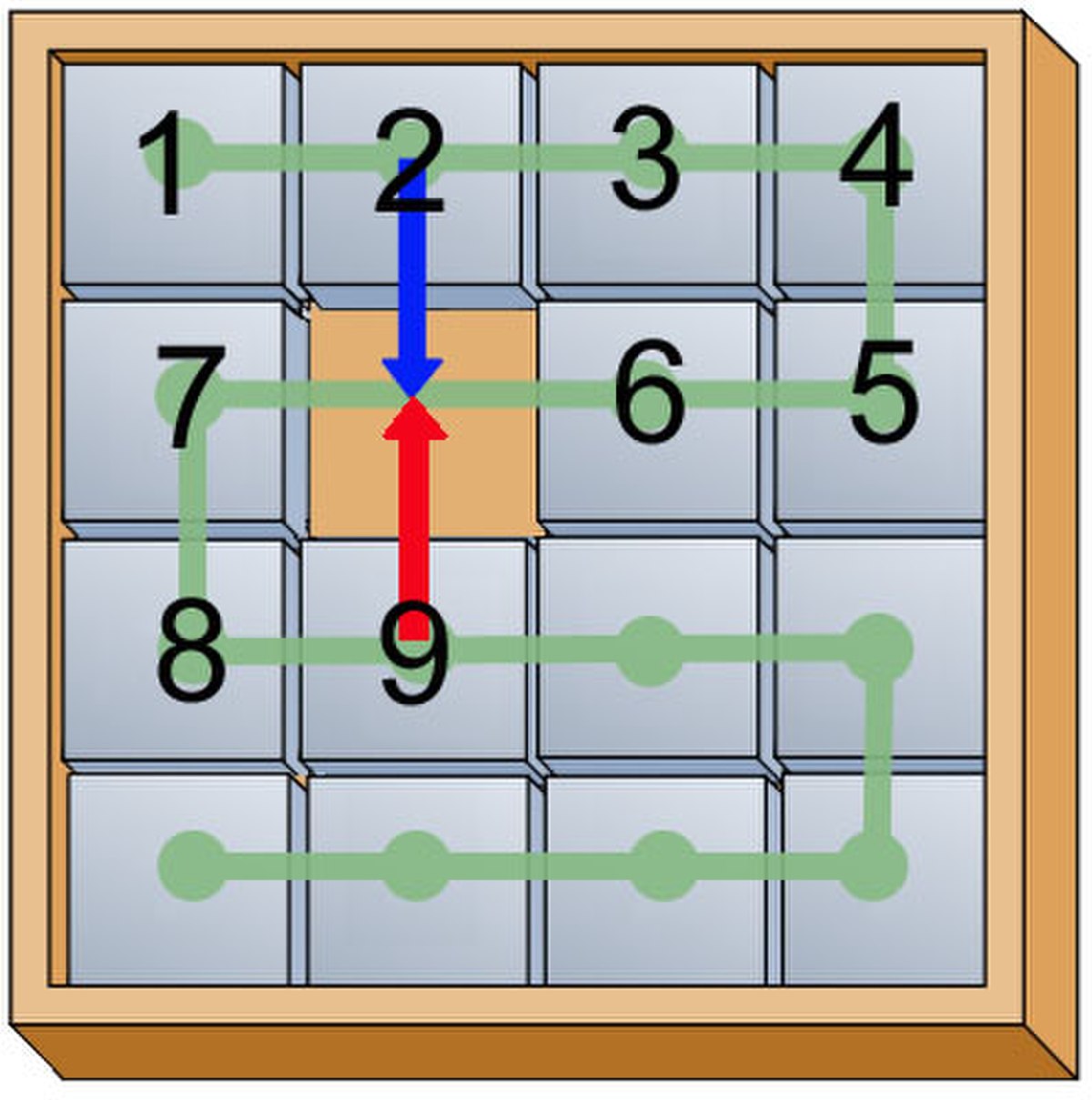
On numérote une position de la manière indiquée par la figure de droite. Le trou n'est pas compté. Ainsi, la position initiale représentée sur la figure est (123456789...). Le mouvement correspondant à la flèche bleue donne la position (134562789...), elle correspond à la permutation (234562), un cycle d'ordre 5 et donc impair. Celle correspondant à la flèche rouge donne (123456978...), elle correspond à la permutation (798) un cycle d'ordre 3, encore impair. Si la case vide est sur un bord, on obtient soit la permutation constante soit une d'ordre 7, encore impair. Ainsi toutes les permutations générant le sous-groupe opérant sur le jeu de taquin sont de signatures paires et font ainsi parti du groupe alterné.
La permutation nécessaire à la résolution du cas de figure intitulée Jeu de taquin non résoluble est une transposition, de signature impaire, elle n'est donc pas réalisable car le groupe alterné ne contient aucune transposition.
Avec les notations utilisées, le cas de figure intitulée Jeu de taquin non résoluble correspond à la position 1,2,3,4,8,7,6,5,9,10,11,12,14,15,13. Celle correspondant au taquin reconstitué dans l'ordre avec la case vide en première position à 1,2,3,7,6,5,4,8,9,10,11,15,14,13,12. Passer de l'une à l'autre des positions impose la permutation (47586)(12 15 13), produit de deux permutations de signature paire, donc paire. Il est ainsi possible de résoudre la question posée par Sam Loyd si l'on permet à la case vide de se trouver en haut à gauche.
La référence sur le taquin montre que le groupe alterné A15 est bien celui qui opère sur le jeu.