Hypernombre - Définition

Introduction

Les hypernombres sont des nombres associés à des dimensions, découverts par le Dr. Charles A. Musès (1919 – 2000). Les hypernombres forment un système complet, cohérent, relié et naturel. Il existe dix niveaux d'hypernombres, chacun possède sa propre arithmétique et géométrie.

Sélection des types d'hypernombres

Nombres réels et complexes

Les deux premiers niveaux de l'arithmétique des hypernombres correspondent à l'arithmétique des réels et nombres imaginaires.

Nombres epsilon

Avec les nombres , le programme des hypernombres est capable de définir un large intervalle d'opérations mathématiques sur les systèmes de nombres contenant des bases avec les racines carrées non-réelles de 1, i.e. mais (voir aussi nombre complexe fendu). Le concept d'orbite de puissance des hypernombres permet les puissances, les racines et les logarithmes sur les systèmes de nombres qui contiennent les bases de .

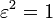
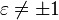
Les nombres epsilon sont placés dans le troisième niveau du programme des hypernombres.

Exponentielle contre-orbite de puissance

Si l'on considére que pour les nombres complexes, l'orbite de puissance i^α ainsi que l'orbite exponentielle du nombre de base imaginaire n'est plus valable, ce n'est pas le cas pour les nombres . A la place, nous avons pour l'orbite exponentielle :

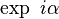
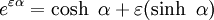
L'orbite de puissance s'écrit :

Note : l'orbite de puissance contient un produit de et , qui requiert l'arithmétique des quaternions coniques (ci-dessous).

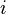
Exemples et isomorphismes

Quaternions circulaires et octonions

Les quaternions et les octonions circulaires du programme des hypernombres sont identiques aux quaternions et aux octonions de la construction de Cayley-Dickson.

Quaternions hyperboliques

Les quaternions hyperboliques issus du programme des hypernombres sont isomorphes aux coquaternions (quaternions fendus). Ils sont différents des quaternions hyperboliques de A. MacFarlane (première mention en 1891), ils ne sont pas associatifs mais ils offrent comme eux un module multiplicatif.

Dans les hypernombres, les quaternions hyperboliques sont constitués d'une base réelle, une base imaginaire et deux bases contre-imaginaires (e.g. {}, ou {}; voir aussi nombre complexe fendu). Comme les quaternions (circulaires), leur multiplication est associative mais non-commutative, les trois bases non-réelles sont mutuellement anti-commutatives.

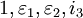
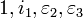
Quaternions coniques

Les quaternions coniques sont construits sur la base {}, avec et forment une arithmétique close commutative, associative, distributive (contenant des racines et des logarithmes), avec un module multiplicatif. Ils contiennent des éléments idempotents et des diviseurs de zéro, mais pas d'éléments nilpotents. Les quaternions coniques sont isomorphes aux tessarines et aussi aux nombres bicomplexes (issus des nombres multicomplexes).

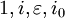
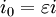
Par contraste, les quaternions et les coquaternions (circulaires) (quaternions fendus) ne sont pas commutatifs (les coquaternions contiennent aussi des éléments nilpotents).

Les quaternions coniques sont nécessaires pour décrire l'orbite de puissance de (ci-dessus) et aussi le logarithme de  :

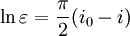
Octonions hyperboliques

Les octonions hyperboliques sont isomorphes à l'algèbre des octonions fendus. Ils sont constitués d'une base réelle, trois bases imaginaires () et quatre bases contre-imaginaire (, ).

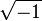
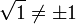
Cette algèbre a été utilisée en physique dans la théorie des cordes. Elle peut être aussi utilisée pour décrire l'équation de Dirac en physique sur un système de nombres naturel (à la place de l'algèbre des matrices sur les nombres complexes; voir les références ci-dessous).

Octonions coniques

Les octonions coniques de bases forment un système de nombre octononique associatif mais non-commutatif.

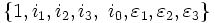
La sous-algèbre est isomorphe aux nombres complexes, avec (pour tout n = 1,2,3), est commutative et associative à toutes les bases de sous-algèbre de quaternion . Les bases des octonions coniques peuvent par conséquent être écrites sous la forme montrant leur isomorphisme aux quaternions avec les coefficients en nombres complexes pour former les biquaternions.

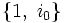
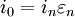
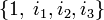
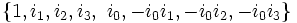
Sédénions coniques

Un cas particulier de l'arithmétique des hypernombres sont les sédénions coniques, qui forment une algèbre modulaire (i.e. avec un module multiplicatif), alternative, flexible, non-commutative; par la construction de Cayley-Dickson, on obtient les octonions (circulaires) (construits sur un axe réel et 7 axes imaginaires), ceci forme une algèbre normée et modulaire la plus large.

Nombres complexes elliptiques (arithmétique w)

Dans le plan (réel, w), l'orbite de puissance (avec réel) est elliptique, et l'arithmétique est, par conséquent aussi appelée complexe elliptique ou nombres w-complexes. Ils sont placés dans le 4^e niveau du programme des hypernombres.

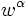
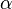
Les puissances de w sont cycliques, avec et les puissances entières suivantes :

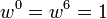
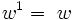
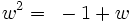
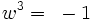
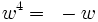
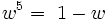
Ils offrent un module multiplicatif :

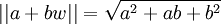
Si a et b sont des coefficients réels, l'arithmétique est un corps. Néanmoins, la base de nombre duale de (w) est (-w), qui est différente du conjugué de (w), qui est 1-(w). Ceci contraste par exemple avec la base imaginaire , pour laquelle le dual et le conjugué sont les mêmes (-i). L'arithmétique résultante (-w) est par conséquent distincte de l'arithmétique -(w), tandis qu'elles coexistent sur le même plan de nombres. Additivement, -(w) et (-w) sont identiques, mais multiplicativement, elles sont distinctes.

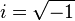
Orbite de puissance

L'orbite de puissance de w est :

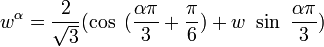
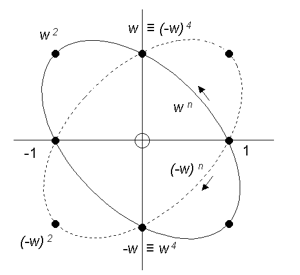
Orbite exponentielle

L'orbite exponentielle de w est (a, b réel) :

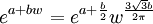
Pour le cas particulier de , l'orbite de puissance et l'orbite exponentielle échouent toutes les deux. Ceci donne :

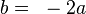
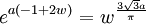
et

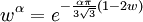
Nombres de rose (nombres p et q)

Les nombres de rose sont placés dans le 5^e niveau dans le programme des hypernombres et forment un quasi système dual. Chacun étant nilpotent, l'arithmétique offre encore un module multiplicatif, un argument et une forme polaire. Géométriquement, les puissances et sont des roses à deux pétales.

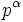
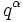
Les puissances entières sont :

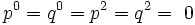
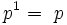
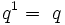
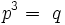
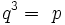
Ils offrent un module multiplicatif :

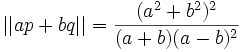
Orbite de puissance

Dans le plan {p, q}, et (avec réel) sont reliés sur une rose à deux pétales, décrite par avec

.

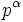
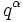
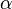
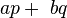
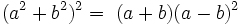
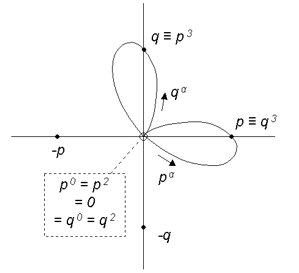
Tandis que le produit pour tout réel {a, b, c, d}, l'orbite de puissance et sa géomérie reliée permet d'effectuer une multiplication non-triviale. Les facteurs peuvent être représentée dans la même orbite de puissance, e.g.

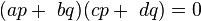
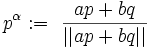
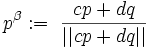
et multiplié plus tard à (avec absolu; , réel). Par conséquent, la multiplication est sensible à la représentation du point dans le plan {p, q}.

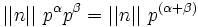
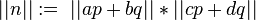
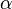
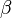
En général, il existe une quantité infinie de représentation possibles de (avec absolu; , réel) pour tout donné. Mais seule la multiplication le long de soit de l'orbite de puissance de p ou de q permet un module multiplicatif.

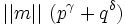
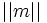
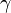
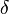
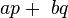
Orbite exponentielle

Les orbites exponentielle respectives sont :

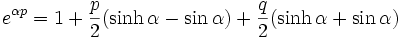
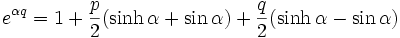
Note sur (-p), p^(-1), 1/p

A partir de C. Musès, Computing in the bio-sciences with hypernumbers: A survey (voir la référence complète ci-dessous) :

"...Notez que -p est engendré via w, ainsi : . Il doit être rappelé que parce que p est nilpotent (), sa puissance zéro-ième ne peut pas être 1; en fait . Par conséquent , et puisque , nous voyons que est panpotent, i.e. une racine de l'infini. A comparer , qui sont une paire de diviseurs de l'infini."

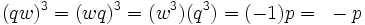
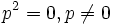
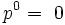
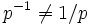
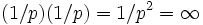
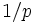
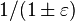
Nombres cassinioïdes (nombres m)

L'arithmétique des nombres cassinioïdes, le 6^e niveau du programe des hypernombres, est gouvernée par les cassinoïdes ou les ovales de Cassini. Leur relation avec la géométrie illustre la multiplication et leur modules multiplicatifs. Les coefficients de la base de nombre m sont des nombres absolus, qui sont similaires aux nombres réels positifs ; néanmoins, l'arithmétique m est sensible à la grandeur de ses coefficients.

Dans le plan {réel, m}, ils offrent les relations suivantes :

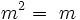
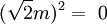
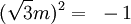
Caractéristique, module et poignée

Pour un nombre , la "caractéristique" s est définie comme suit :

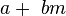
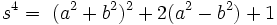
Un module multiplicatif t et une poignée k sont alors défini à travers :

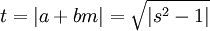
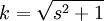
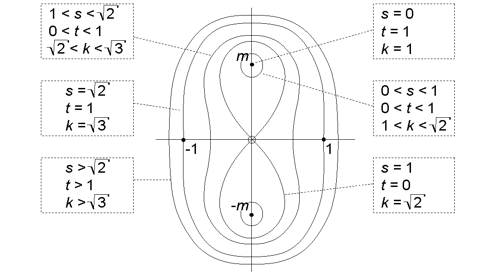
Distinction entre coefficients et nombres réels

En citant K. Carmody, "Cassinoid Numbers: The Musèan Hypernumber m" (27 avril 2006, sur http://www.kevincarmody.com/math/hypernumbers.html ):

« Les coefficients tels que dans l'expression ne sont pas véritablement des nombres réels. Par exemple, si nous multiplions -1 comme un nombre réel par + m, nous pouvons obtenir , mais nous ne pouvons pas obtenir . [...]

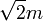
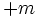
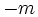
De manière correcte, +1, -1, +m et -m sont des unités, et les coefficients de leurs multiples le long de leurs axes respectifs sont des nombres absolus, qui sont distincts des nombres réels et qui ne sont jamais négatifs. »