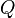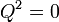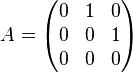Nilpotent - Définition
En mathématiques, un élément x d'un anneau R est appelé nilpotent s'il existe un certain nombre entier positif n tel que
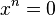
Exemples
Cette définition peut être appliquée en particulier aux matrices carrées. La matrice
est nilpotente parce que
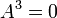
Dans l'anneau ?/9?, la classe de 3 est nilpotente parce que
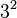
L'anneau des coquaternions contient un cône de nilpotents.
Propriétés
Aucun élément nilpotent ne peut être une unité (excepté dans l'anneau trivial {0} qui possède seulement un élément unique 0 = 1). Tous les éléments nilpotents différents de zéro sont des diviseurs de zéro.
Une matrice carrée d'ordre n à coefficients dans un corps commutatif est nilpotente si et seulement si son polynôme caractéristique est
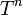
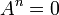
Les éléments nilpotents d'un anneau commutatif forment un idéal, qui est le nilradical de l'anneau.
Si x est nilpotent, alors 1 - x est une unité, parce que
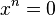
-
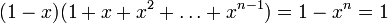
En physique
Un opérateur