Iconographie des corrélations - Définition
La liste des auteurs de cet article est disponible ici.
Qu’est-ce qu’une corrélation « remarquable » ?
Une forte corrélation n’a pas de sens isolément. Réciproquement une faible corrélation n’implique pas l’absence de lien.
- Exemple 1
Les variables A et C sont fortement corrélées parce que leurs variations sont toutes les deux liées à une variable X. En réalité il n’y a pas de lien AC, mais un lien XA et un lien XC. En d’autres termes, la corrélation entre A et C est redondante, et elle disparaît lorsque X est maintenu constant (on parle de « corrélation partielle » faible par rapport à X). D’où le schéma des seules corrélations remarquables :
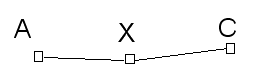
- Exemple 2
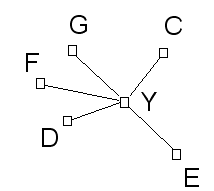
La variable Y dépend de plusieurs variables C, D, E, F et G indépendantes. Aussi la corrélation de Y avec chacune d'entre elles, prise séparément, est faible (non « significative » au sens probabiliste du terme). En réalité, il existe les liens rigoureux CY, DY, EY, FY et GY. D’où le schéma des corrélations remarquables :
Algorithme de l’iconographie des corrélations
Si le tableau de données est petit, le principe de l’iconographie des corrélations est suffisamment simple pour permettre un tracé manuel. Sinon, il faut recourir à un programme comportant, en entrée, la matrice de corrélation et le seuil choisi (par exemple 0,3). En voici l’algorithme :
- Pour éviter les redondances, le lien AB est tracé si et seulement si la corrélation totale r(A,B) est supérieure au seuil en valeur absolue, et si les corrélations partielles r(A,B), par rapport à une variable Z, sont supérieures au seuil, en valeur absolue, et de même signe que la corrélation totale, pour tout Z parmi les variables disponibles, y compris les « instants ».
Ce critère de tracé, sévère, garantit la sélection des liens les plus « solides ».
Les variables peuvent être quantitatives et/ou qualitatives (pourvu que ces dernières utilisent un codage disjonctif complet).
Instants remarquables de l’analyse
Les données disponibles permettent de pousser plus loin l’analyse.
On peut considérer en effet chaque ligne comme un « instant » de l’analyse, caractérisé par une variable indicatrice, égale à 1 à l’instant de la ligne considérée, et à 0 sinon :
| Élève | Poids | Âge | Assiduité | Note | e1 | e2 | e3 | e4 | e5 | e6 | e7 | e8 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| e1 | 52 | 12 | 12 | 5 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| e2 | 59 | 12,5 | 9 | 5 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| e3 | 55 | 13 | 15 | 9 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| e4 | 58 | 14,5 | 5 | 5 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| e5 | 66 | 15,5 | 11 | 13,5 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| e6 | 62 | 16 | 15 | 18 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| e7 | 63 | 17 | 12 | 18 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| e8 | 69 | 18 | 9 | 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
Bien que les « instants » portent les mêmes noms que les élèves, il faut se rappeler que les élèves sont des lignes (des observations), tandis que les instants sont des colonnes, qui font partie des « variables », au même titre que les 4 premières colonnes.
Nous pouvons donc adopter le même critère de tracé des liens pour les « instants » et les variables originelles. Toutefois, pour ne pas alourdir le schéma, dessinons seulement les « instants » liés à une variable au moins (« instants remarquables ») :
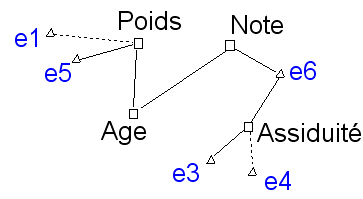
Les « instants » sont représentés par un triangle, pour être mieux distingués des variables originelles, qui sont représentées par un carré.
- Par rapport au schéma précédent, le lien entre note et assiduité a disparu, remplacé par les liens (Note,e6) et (Assiduité,e6) . Il était donc redondant : l’élève e6, très assidu et bien noté, explique à lui tout seul le lien (Note,Assiduité).
- L’élève e3 a une assiduité remarquablement forte, et l’élève e4 une assiduité remarquablement faible (trait pointillé).
Un lien est dit « remarquable » quand les autres liens présents sur la figure ne suffisent pas à l’expliquer.
- L’élève e6 a en effet une note « remarquable » : 18/20.
- Les élèves e7 et e8 qui ont, eux aussi, 18/20, ne sont pas remarquables : ils n’apparaissent pas sur le schéma, car, plus âgés, leur note est déjà expliquée par le lien (âge,note).
- De la même façon, on peut vérifier sur les données, que e5 a un poids remarquablement fort pour son âge (par rapport aux 8 élèves de la population étudiée) ; tandis que l’élève e1 à un poids remarquablement faible pour son âge.
Les liens entre carrés (variables-variables) soulignent les lois générales; les liens carré-triangle (variable-instant) soulignent les événements rares.

















































