Iconographie des corrélations - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En analyse des données, l'iconographie des corrélations est une méthode qui consiste à remplacer une matrice de corrélation par un schéma où les corrélations « remarquables » sont représentées par un trait plein (corrélation positive), ou un trait pointillé (corrélation négative).
Cette idée apparaît aussi dans les modèles graphiques gaussiens utilisés notamment en cartographie du génome. Mais l’iconographie des corrélations est plus générale en ce qu’elle ne fait pas d’hypothèse sur la distribution gaussienne, ou non, des variables, et repose uniquement sur l’aspect géométrique du coefficient de corrélation.
Historique
L’idée première de l’iconographie des corrélations remonte à 1975. Appliquée d’abord à la géochimie marine, elle fit l’objet d’une thèse d’état en 1981, et d’un article dans les Cahiers de l’Analyse des Données en 1982. Après cela, l’application de la méthode dans de nombreuses branches de l’industrie aérospatiale pendant une quinzaine d’année, explique, paradoxalement, la relative confidentialité dans laquelle elle est restée longtemps, les entreprises ne souhaitant pas en général crier leurs solutions sur les toits. Depuis la création en 1997 d’une première société diffusant un logiciel basé sur l’iconographie des corrélations, et son enseignement dans certaines universités, la bibliographie s’est largement étendue, en particulier dans les secteurs médical et astrophysique (spectrométrie de masse).
Cette présentation, à visée pédagogique, s'inspire des documents cités en référence.
Sélection des liens remarquables
Illustrons-la sur un petit exemple : Lors d’un contrôle mathématique d'un niveau de classe de troisième, huit élèves de la sixième à la terminale, dont nous connaissons le poids, l'âge et l’assiduité, ont obtenu les notes suivantes :
| Élève | Poids | Âge | Assiduité | Note |
|---|---|---|---|---|
| e1 | 52 | 12 | 12 | 5 |
| e2 | 59 | 12,5 | 9 | 5 |
| e3 | 55 | 13 | 15 | 9 |
| e4 | 58 | 14,5 | 5 | 5 |
| e5 | 66 | 15,5 | 11 | 13,5 |
| e6 | 62 | 16 | 15 | 18 |
| e7 | 63 | 17 | 12 | 18 |
| e8 | 69 | 18 | 9 | 18 |
| Poids | Âge | Assiduité | Note | |
| Poids | 1 | |||
| Âge | 0,885 | 1 | ||
| Assiduité | -0,160 | -0,059 | 1 | |
| Note | 0,774 | 0,893 | 0,383 | 1 |
Plaçons les quatre variables au hasard sur le papier, et traçons un trait entre deux d’entre elles chaque fois que leur corrélation est supérieure au seuil de 0,3 en valeur absolue.
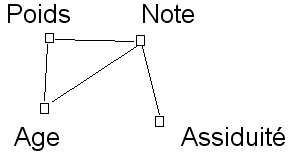
Au vu de ce schéma, la corrélation (poids,note) = 0.774, relativement forte, donne à penser que le poids a plus d’influence sur la note que l’assiduité ! Mais, d’autre part, nous avons les corrélations (poids,âge) = 0,885, et (âge,note) = 0,893.
À partir de ces 3 coefficients de « corrélation totale », la formule de la « corrélation partielle » donne : Corrélation (poids,note) à âge constant : = -0,08
La corrélation entre note et poids, à âge constant a fortement baissé (elle est même légèrement négative). En d’autres termes, le poids n’a pas d’influence sur la note. Cela n’est guère surprenant. Effaçons le lien entre poids et note :
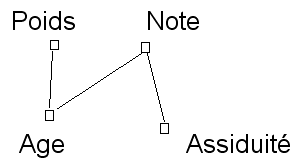
En définitive, un lien n’est pas tracé,
- soit parce que sa corrélation totale est inférieure au seuil, en valeur absolue,
- soit parce qu’il existe au moins une corrélation partielle inférieure au seuil, en valeur absolue, ou de signe contraire à la corrélation totale.
Il n’y a pas lieu, ici, d’effacer d’autres liens, comme on le vérifie à partir des valeurs des autres corrélations partielles :
-
- Corrélation (poids,note) à assiduité constante : = 0,92
- Corrélation (âge,poids) à note constante : = 0,68
- Corrélation (âge,poids) à assiduité constante : = 0,89
- Corrélation (âge,note) à poids constant : = 0,71
- Corrélation (assiduité,poids) à note constante : = -0,78
- Corrélation (assiduité,poids) à âge constant : = -0,23
- Corrélation (assiduité,note) à poids constant : = 0,81
- Corrélation (assiduité,note) à âge constant : = 0,97
- Corrélation (assiduité,âge) à poids constant : = 0,18
- Corrélation (assiduité,âge) à note constante : = -0,97
Puisque le nombre de variables est m = 4, il y a m.(m-1)/2 = 6 couples distincts de variables et, pour chaque couple, (m-2) = 2 coefficients de corrélation partielle.
Soulignons ici une différence importante entre l’Iconographie des Corrélations et le modèle graphique gaussien :
Nous venons de voir que l’iconographie des corrélations s’appuie sur (m-2).m.(m-1)/2 = 12 coefficients de corrélations partielles, calculés, chacun, par rapport à une seule variable, donc sans mélanger les effets de chacune d’elles. Au contraire le modèle graphique gaussien repose sur les seuls m.(m-1)/2 = 6 coefficients de corrélations partielles par rapport aux (m-2) autres variables. Il agrège donc une multiplicité de relations triangulaires et en retient une sorte de moyenne (matrice de corrélation partielle de chaque couple de variable par rapport à toutes les autres variables). Il perd la mise en évidence d’une variable particulière expliquant ou infirmant la relation entre deux variables.
L’iconographie des corrélations permet donc d’augmenter à la fois la quantité et la qualité de l’information utilisée.

















































