Iconographie des corrélations - Définition

Choix du seuil

Le seuil peut varier entre 0 et 1. Un lien n'est tracé que si, non seulement la corrélation totale, mais encore toutes les corrélations partielles correspondantes, sont supérieures au seuil en valeur absolue, et de même signe. Cette condition est sévère, et les liens qui subsistent sont, en général, riches d’information.

Augmenter la valeur du seuil diminue le nombre de liens, et clarifie la figure, mais diminue aussi l’information, surtout quand la variable d’intérêt dépend de plusieurs variables indépendantes.

Il est souvent préférable de prendre un seuil assez bas. Puis, si la figure complète est trop touffue, de ne dessiner que les liens à la variable d’intérêt.

À titre d’exemple, lorsqu’on aborde de nouvelles données, et qu’on ne sait pas quel seuil choisir, on pourra commencer par :

• un seuil = 0.3 pour une analyse de données ;
• un seuil = 0.1 pour l’analyse des résultats d’un plan d’expériences. Dans ce cas en effet, tous les facteurs sont contrôlés, et l’on peut se permettre de ne pas dessiner les « instants » (a priori remarquables par construction du plan), ce qui allège la figure ;
• un seuil = 0.01, ou moins, pourra même être choisi lorsque le tableau de données comprend plusieurs centaines d’observations.

Dans notre exemple, même au seuil nul, le lien (poids,note) n’est pas tracé, car la corrélation partielle par rapport à l’âge est de signe contraire à la corrélation totale. Mais le lien (assiduité,note) apparaît, et il y a plus d’instants remarquables.

Position des points sur le papier

L‘exemple ci-dessus a montré deux sortes de points : les variables (carrés), et les « instants » (triangles). Une fois trouvé les liens entre ces éléments, positifs (traits pleins) ou négatifs (traits pointillé), il reste à les dessiner sur le papier.

Toute latitude de positionnement est laissée à l’analyste, puisque l’interprétation dépend des liens et non des positions.

Autant que possible, il faut éviter les croisements inutiles entre liens, gênant la lecture. Le schéma suivant, par exemple, est moins lisible que le précédent, bien que l’interprétation soit la même (liens identiques) :

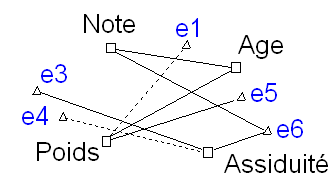
Plusieurs approches peuvent être utilisées pour disposer les points de façon automatique.

Une première approche consiste à projeter le nuage de points des variables sur les deux premiers axes d’une analyse en composantes principales. Mais les projections ne sont pas toujours adaptées à une bonne lisibilité lorsqu’il y a beaucoup de composantes principales statistiquement significatives, et particulièrement en cas de mélange de variables qualitatives et quantitatives.

Une deuxième approche repose sur les algorithmes de force (Kamada-Kawai ou Fruchterman et Reingold par exemple) qui simulent un système de ressorts sur les arêtes du graphe : la définition d'une force répulsive entre les arêtes, et d'une force attractive ente les arêtes connectées permet d'obtenir un équilibre. Le dessin est en général satisfaisant pour les structures arborescentes, mais, au-delà de quelques dizaines de sommets, la compréhension est difficile en cas de structures bouclées sur plusieurs dimensions.

Enfin, une troisième approche consiste à tirer parti de l’interprétation géométrique du coefficient de corrélation (cosinus), et à dessiner le schéma à la surface d’une sphère à 3 dimensions :

• L'arc-cosinus de la corrélation étant une distance angulaire, deux points seront d’autant plus proches sur la sphère qu’ils seront plus corrélés (positivement). Inversement, la distance angulaire entre deux points corrélés négativement est un angle obtus ; si la corrélation vaut -1, les points sont opposés sur la sphère (angle 180°).
  Il s’agit d’un pis aller, car la sphère réelle n’est pas à 3 dimensions, mais à n dimensions. Si donc deux points très corrélés sont forcément proches sur le dessin, l’inverse n’est pas sûr : deux points très proches sur le dessin ne sont pas forcément corrélés. Toutefois, l’absence de lien tracé lève l’ambiguïté.
• On pourrait envisager bien d’autres modes de choix des positions : le plus utilisé consiste à choisir comme distance angulaire l’arc-cosinus de la valeur absolue de la corrélation. Ainsi les points corrélés négativement ne sont pas opposés sur la sphère, et le lien pointillé est plus court et encombre moins le schéma.
  En pratique, dans une approche logicielle, une première variable A est dessinée n'importe où sur la sphère. Puis la variable B la moins corrélée à cette première est posée sur la sphère à la distance arc-cosinus(r(A,B)) de la première. On place alors, par triangulation, la variable C la moins corrélée aux deux premières. Les autres points sont posés de proche en proche. Si la quatrième variable a une corrélation nulle avec les trois premières, il n'est matériellement pas possible de lui assigner une position exacte. Les distances sont recalculées de façon proportionnelle aux valeurs réelles. Au bout d'un certain temps, la position des premiers points est recalculée d'après les suivants. Etc. Ainsi, la figure est réajustée progressivement.
• L’algorithme, qui s’ajuste autant que possible aux distances réelles, n’est donc pas bloqué si la structure se déploie dans plus de trois dimensions. Et, même si elle contient plusieurs milliers de variables, il est toujours possible d’en prendre un extrait qui peut s’étaler à la surface de la sphère pour sauvegarder la lisibilité. Etant déterministes, puisque les positions sur la sphère à n dimensions sont connues avec certitude, les calculs sont rapides.