Iconographie des corrélations - Définition
La liste des auteurs de cet article est disponible ici.
Interactions logiques remarquables
De même que les « instants » sont rajoutés, ci-dessus, au tableau initial, comme de nouvelles colonnes, de même on peut rajouter d’autres colonnes, par exemple des fonctions des variables initiales, en particulier des « interactions logiques », qui sont des couplages de variables.
Le nombre de colonnes supplémentaires importe peu, pourvu qu’on ne rajoute sur le schéma que celles qui seront liées à l’une au moins des variables initiales, afin de ne pas alourdir inutilement la figure.
Par exemple, suite à l’ajout de nouvelles colonnes correspondant au « & » logique entre deux variables quelconques, seule l’interaction « Age&Assiduité » apparaît directement liée à la note :
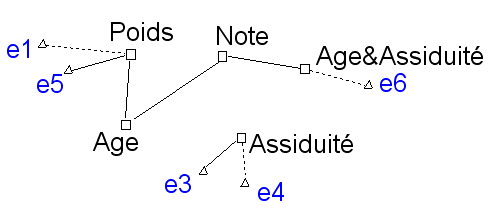
L’interaction logique apporte quelque chose de plus à l’interprétation (compte tenu du petit nombre de variables explicatives disponibles dans cet exemple) : pour obtenir une bonne note il ne suffit pas d’être plus âgé, il faut aussi être assidu au cours.
Champs d’application de l’iconographie des corrélations
Un moyen de ne rien oublier d’essentiel dans un tableau de donnée
Le tableau suivant est difficile à appréhender d’un coup d’œil :
| Mercure | Vénus | Terre | Mars | Jupiter | Saturne | Uranus | Neptune | |
|---|---|---|---|---|---|---|---|---|
| DistanceSoleil | 0.387099 | 0.723332 | 1 | 1.523662 | 5.203363 | 9.53707 | 19.19126 | 30.06896 |
| Rayon | 0.3825 | 0.9488 | 1 | 0.53226 | 11.209 | 9.449 | 4.007 | 3.883 |
| Surface | 0.1471 | 0.901 | 1 | 0.2745 | 125.5 | 86.27 | 15.88 | 15.1 |
| Volume | 0.056 | 0.87 | 1 | 0.151 | 1321.3 | 763.59 | 63.086 | 57.74 |
| Masse | 0.055 | 0.815 | 1 | 0.107 | 318 | 95 | 14 | 17 |
| Densité | 5.43 | 5.24 | 5.515 | 3.94 | 1.33 | 0.697 | 1.29 | 1.76 |
| Gravité | 3.7 | 8.87 | 9.81 | 3.71 | 23.12 | 8.96 | 8.69 | 11 |
| VitesseDeLibération | 4.25 | 10.36 | 11.18 | 5.02 | 59.54 | 35.49 | 21.29 | 23.71 |
| PériodeRotation | 58.64622 | -243.018 | 0.997269 | 1.025957 | 0.41354 | 0.44401 | -0.7183 | 0.67125 |
| PériodeOrbitale | 0.240847 | 0.615197 | 1.000017 | 1.880848 | 11.86261 | 29.4475 | 84.01685 | 164.7913 |
| VitesseOrbitale | 47.8725 | 35.0214 | 29.7859 | 24.1309 | 13.0697 | 9.6724 | 6.8352 | 5.4778 |
| Excentricité | 0.205631 | 0.006773 | 0.016710 | 0.093412 | 0.048392 | 0.054150 | 0.047167 | 0.008585 |
| Inclinaison | 7.00487 | 3.39471 | 0.00005 | 1.85061 | 1.3053 | 2.48446 | 0.76986 | 1.76917 |
| InclinaisonAxiale | 0 | 177.3 | 23.45 | 25.19 | 3.12 | 26.73 | 97.86 | 29.58 |
| TempératureSurface | 166.85 | 456.85 | 17.35 | -46 | -121.15 | -139.15 | -197.15 | -220.15 |
| He | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| Na | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| P | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| CO | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| N | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| O | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| Ar | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| H | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| CH | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| NombreLunesConnues | 0 | 0 | 1 | 2 | 63 | 60 | 27 | 13 |
| Anneaux | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| DiscriminantPlanétaire | 9.1 | 135 | 170 | 18 | 62.5 | 19 | 2.9 | 2.4 |
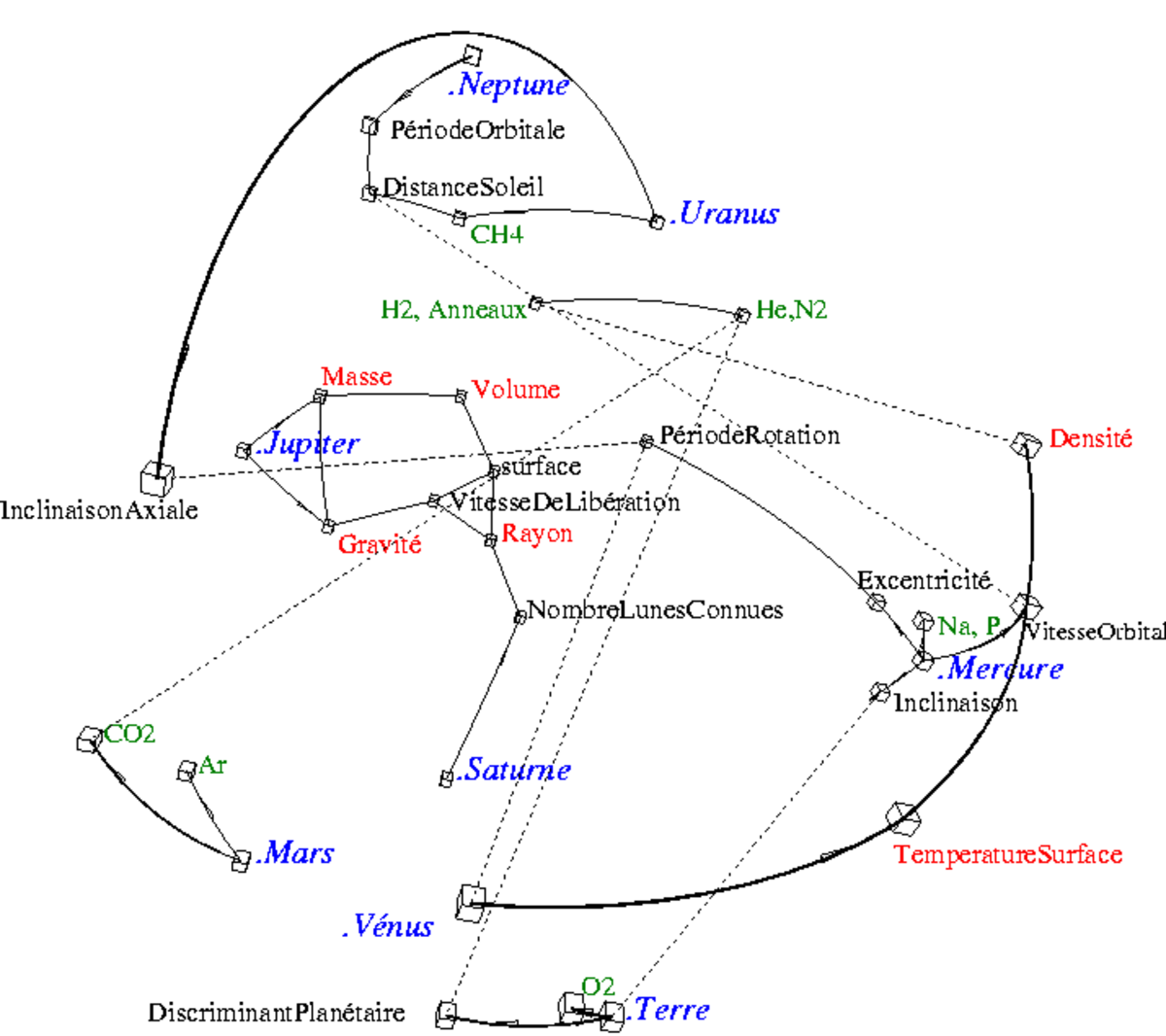
La figure montre les liens plus ou moins évidents (comme celui de la gravité avec la vitesse de libération) ; et aussi les liens propres à chaque planète.
C’est un moyen de ne rien oublier d’important.
Par exemple, les liens de la figure s'interprètent comme suit:
- Les planètes à forte vitesse orbitale (comme Mercure) ont aussi une forte densité et une forte température (en particulier Vénus).
- La Terre a une faible inclinaison (trait pointillé), beaucoup d’O dans son atmosphère, et un fort discriminant planétaire (traits pleins).
- Une plus grande période de rotation correspond à une faible inclinaison axiale et à une forte excentricité.
- Etc.
On pourrait augmenter le nombre de liens remarquables en baissant le seuil du tracé. Il faudrait alors, pour garder un dessin lisible, n'en dessiner qu'une partie: par exemple les liens à une variable d'intérêt.
L’analyse des grands tableaux de bord
Le tableau de bord de gestion est un moyen d’analyse et de diagnostic. Constitué de plusieurs indicateurs de performance, il permet de connaître la charge de travail, d’apercevoir l’hypertrophie ou l’atrophie d’exécution des différentes tâches, de situer les anomalies de fonctionnement, de redresser certaines situations. Cependant, compte tenu des limites de notre mémoire, un tableau de bord doit comporter peu de chiffres pour être d’emploi facile.
L’iconographie des corrélations est un moyen d’analyser un tableau de bord qui a beaucoup de chiffres, et d’exploiter vraiment toutes les informations de l’entreprise. Pouvant s’affranchir des influences extérieures (telles que tendances économiques ou décisions de marketing), elle permet de mieux mettre en évidence l’influence mutuelle des tâches, d’analyser les causes d’écart entre prévision et réalisation, et, grâce au schéma synthétique, de faire remonter rapidement l’information brute sous forme de préconisations opérationnelles.
Une alternative à la stratification
La stratification consiste à découper la base de données en groupes homogènes (strates). Dans l’exemple examiné plus haut, la stratification consisterait à faire des groupes d’élèves de même âge, et des sous-groupes d’élèves de même assiduité. Cela permettrait de s’affranchir, dans chaque groupe de l’effet de l’âge, et dans chaque sous-groupe de l’effet de l’assiduité. Malheureusement tous nos élèves ont un âge différent !
En fait, stratifier n’est intéressant que si la variable de stratification est corrélée au paramètre d’intérêt. De plus, les strates ne doivent pas être vides. Il n’est donc pas possible de stratifier sur beaucoup de variables ou sur une faible population.
L’iconographie des corrélations, au contraire, permet de s’affranchir de l’effet de l’âge même si la stratification est impossible, pourvu que l’âge soit connu.
C’est pourquoi, en iconographie des corrélations, un grand nombre de variables en rapport avec le problème ne complique pas l’analyse. Au contraire, il ne peut qu’affiner la représentation. Il est donc recommandé de commencer d’emblée l’analyse sur toutes les variables disponibles : c’est le moyen de s’affranchir le plus tôt possible des « fausses bonnes corrélations » qui peuvent nous engager sur de fausses pistes (biais, facteurs de confusions).