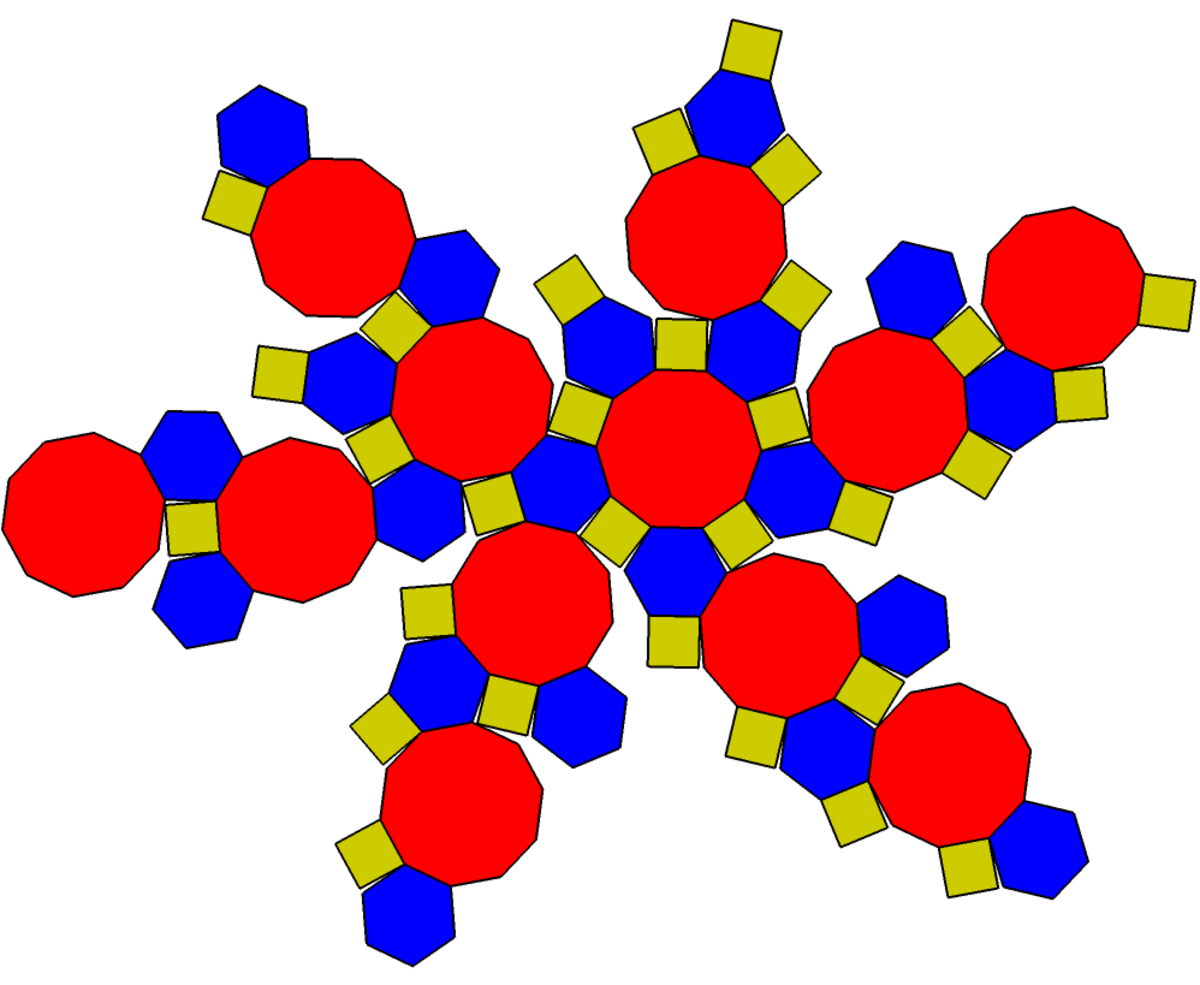
Icosidodécaèdre tronqué - Définition

Introduction

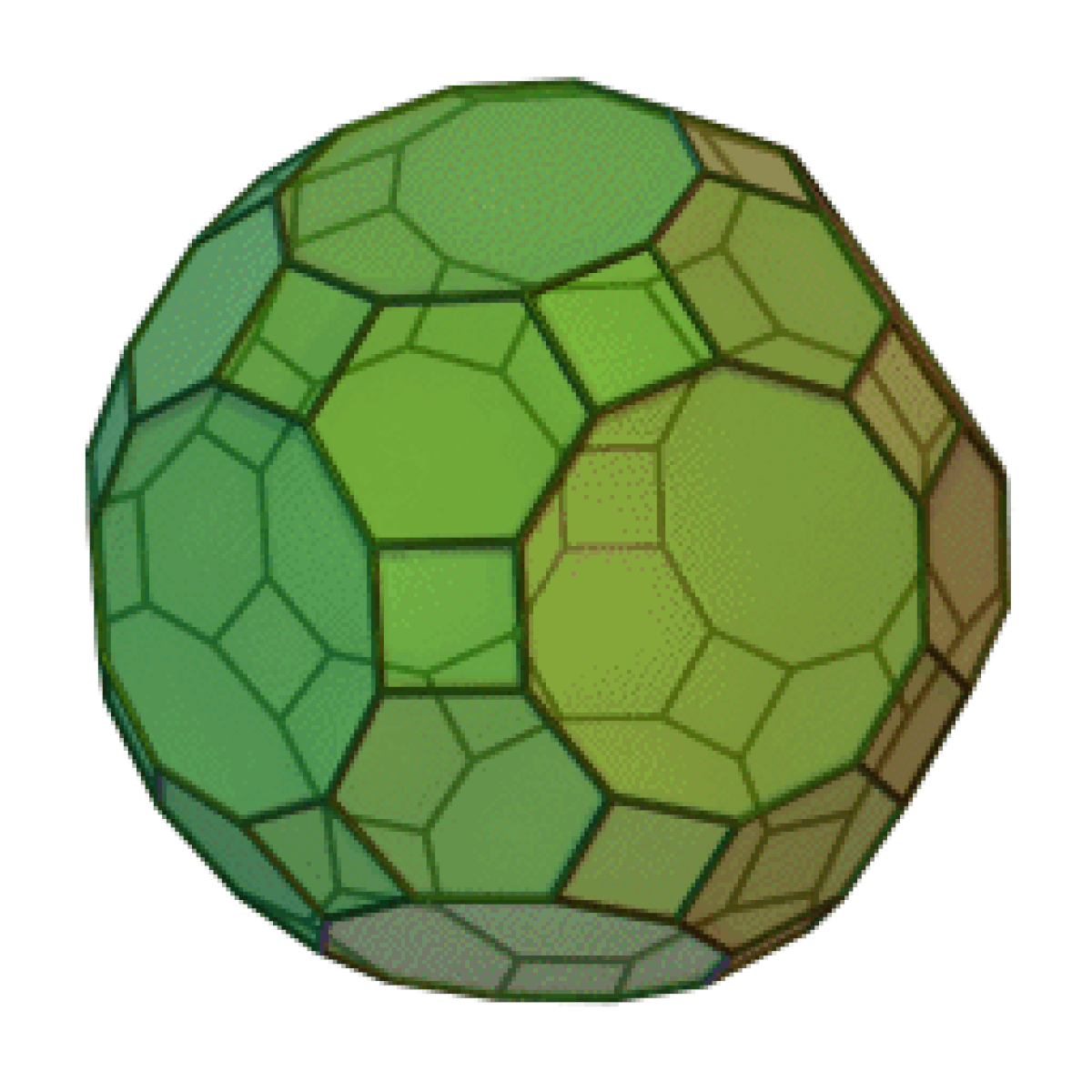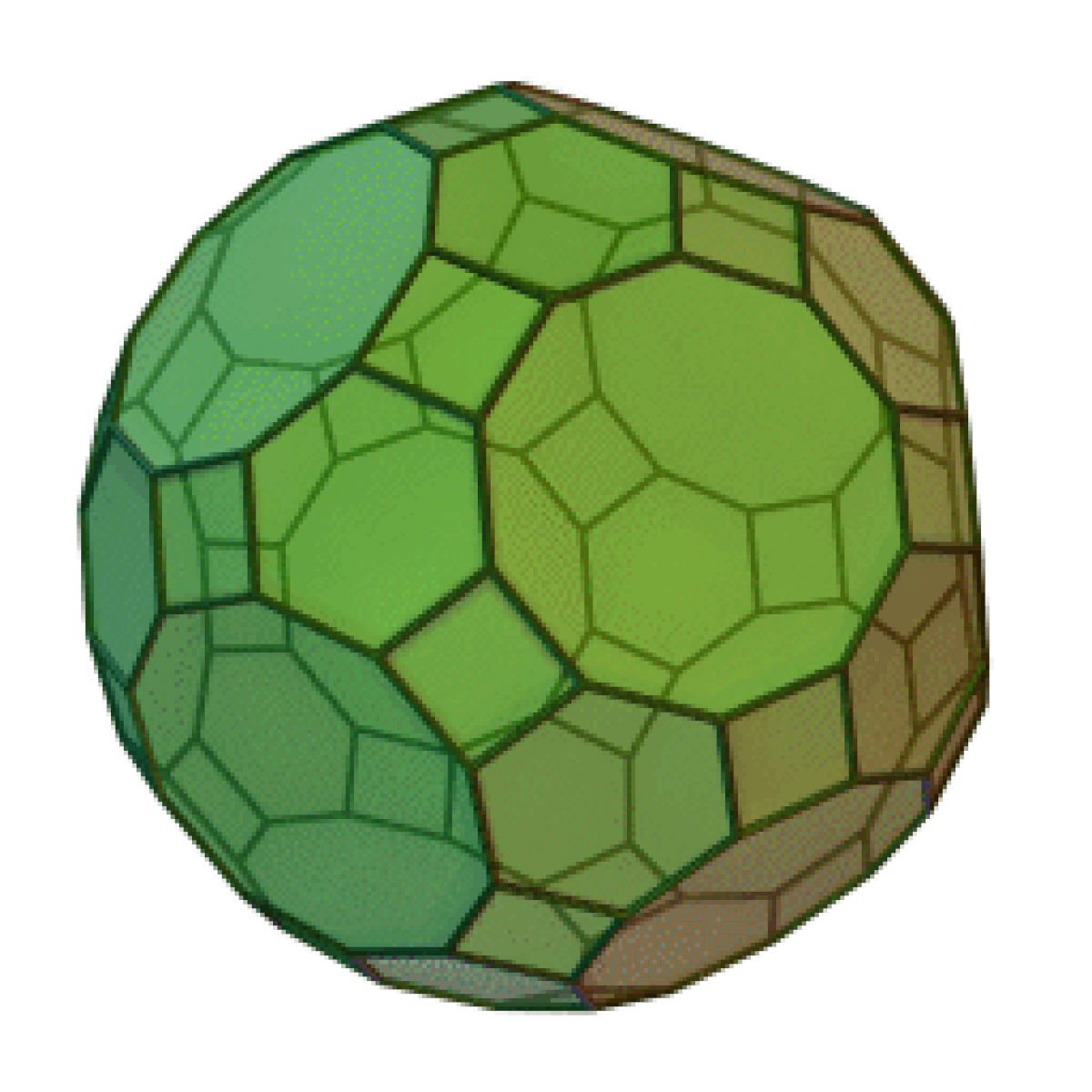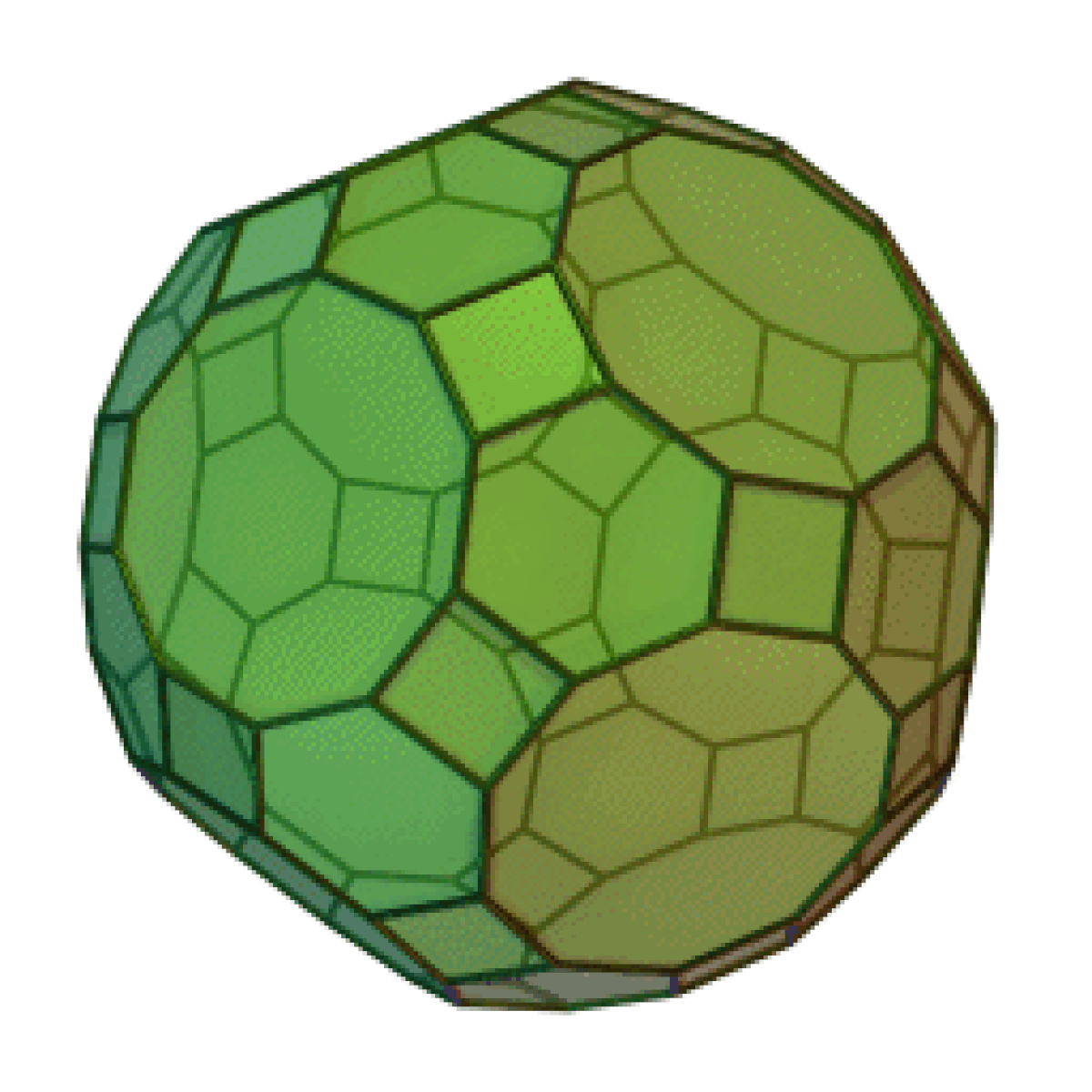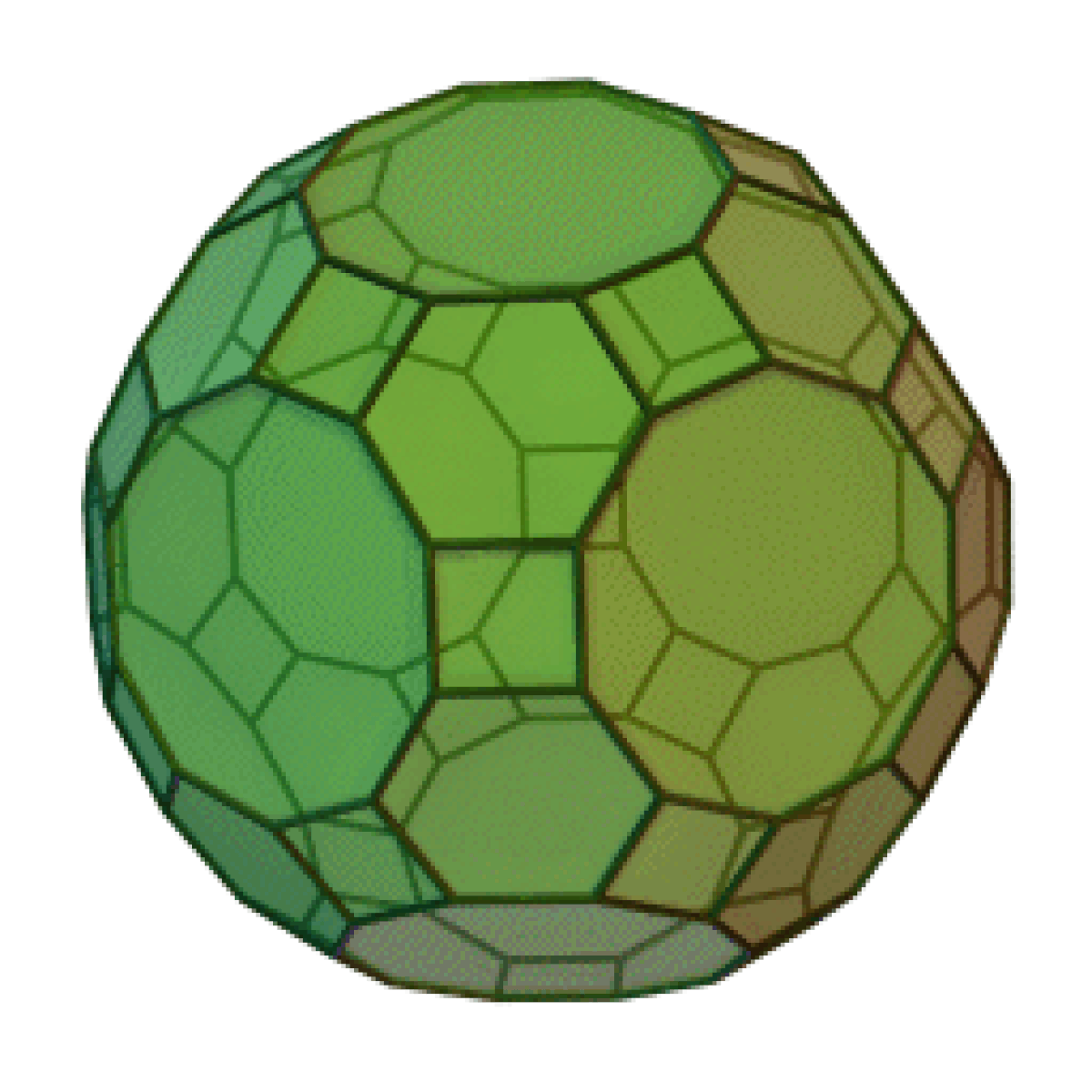
Grand rhombicosidodécaèdre
Type	Solide d'Archimède
Faces	Carrés, Hexagones et Décagones
Éléments :  · Faces  · Arêtes  · Sommets  · Caractéristique	62 180 120 2
Faces par sommet	3
Sommets par face	4, 6 et 10
Isométries	I
Dual	Hexaki icosaèdre
Propriétés	Semi-régulier et convexe, zonoèdre
modifier

Patron (géométrie)

Le grand rhombicosidodécaèdre est un solide d'Archimède. Il possède 30 faces carrées régulières, 20 faces hexagonales régulières, 12 faces décagonales régulières, 120 sommets et 180 arêtes. Puisque chacune des faces possède un centre de symétrie (ou de manière équivalente une rotation à 180°), le grand rhombicosidodécaèdre est un zonoèdre.

Autres noms

D'autres noms incluent :

• Grand rhombicosidodécaèdre
• Icosidodécaèdre rhombitronqué
• Icosidodécaèdre omnitronqué

Le nom Icosidodécaèdre tronqué, donné à l'origine par Johannes Kepler est inexact. Si vous tronquez un icosidodécaèdre en coupant les coins, vous n'obtenez pas cette figure uniforme : certaines faces seront des rectangles. Néanmoins, la figure résultante est topologiquement équivalente à celle-ci et peut toujours être déformée jusqu'à ce que les faces soient régulières.

Le nom grand rhombicosidodécaèdre (de même que Icosidodécaèdre rhombitronqué) fait référence au fait que les 30 faces carrées sont placées dans les mêmes plans que les 30 faces du triacontaèdre rhombique qui est le dual de l'icosidodécaèdre. À comparer avec le petit rhombicosidodécaèdre.

Une source malheureuse de confusion : il existe un polyèdre uniforme non-convexe avec le même nom. Voir le grand rhombicosidodécaèdre uniforme.

Coordonnées cartésiennes

Les coordonnées cartésiennes pour les sommets d'un grand rhombicosidodécaèdre centré à l'origine sont toutes les permutations paires de

(±1/τ, ±1/τ, ±(3+τ)),

(±2/τ, ±τ, ±(1+2τ)),

(±1/τ, ±τ², ±(-1+3τ)),

(±(-1+2τ), ±2, ±(2+τ)) et

(±τ, ±3, ±2τ),

où τ = (1+√5)/2 est le nombre d'or.