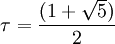Petit rhombicosidodécaèdre - Définition

Introduction

Petit rhombicosidodécaèdre
Type	Solide d'Archimède
Faces	Triangles, Carrés et Pentagones
Éléments :  · Faces  · Arêtes  · Sommets  · Caractéristique	62 120 60 2
Faces par sommet	4
Sommets par face	3, 4 et 5
Isométries	I
Dual	Hexacontaèdre trapézoïdal
Propriétés	Semi-régulier et convexe
modifier

Patron

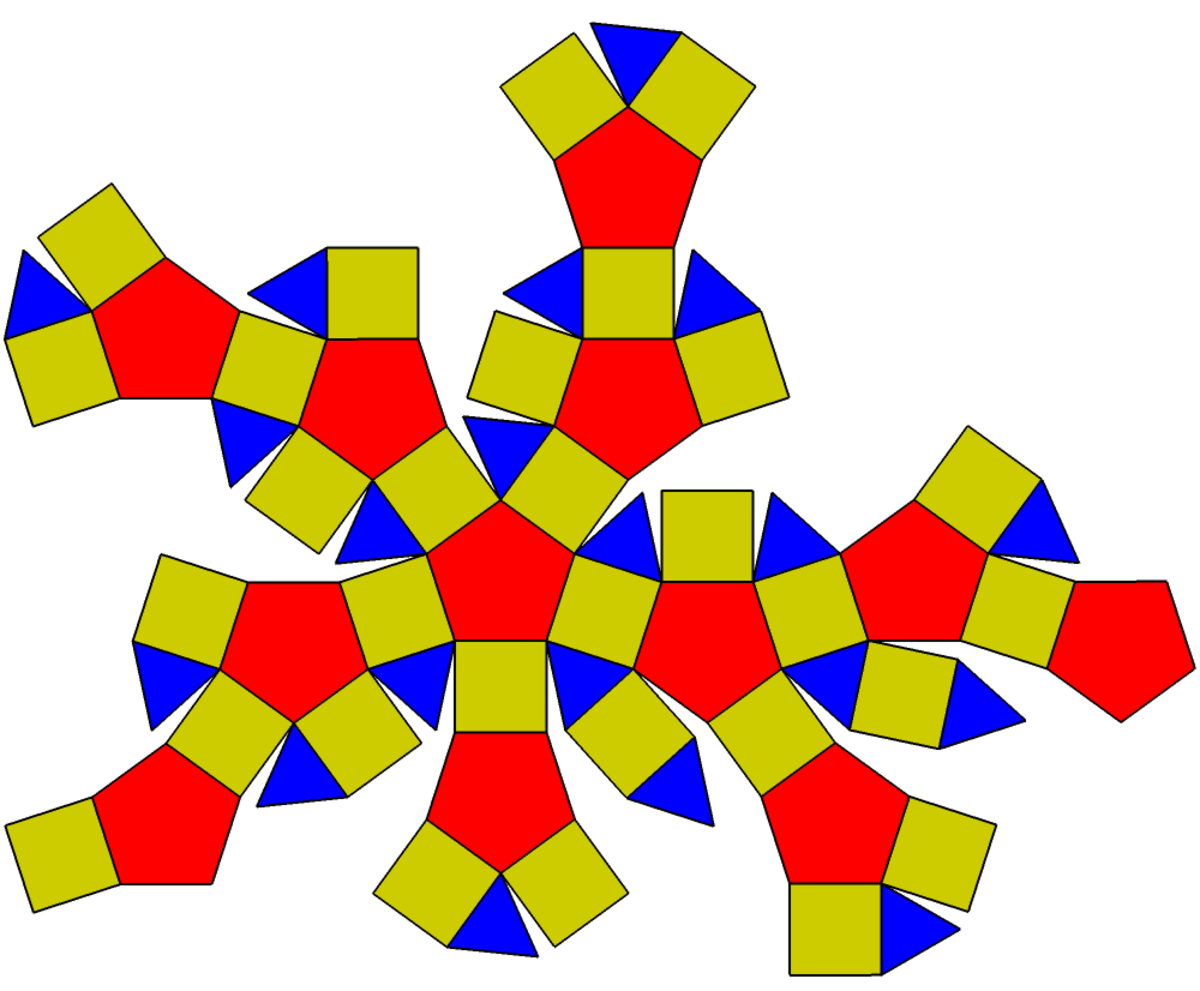
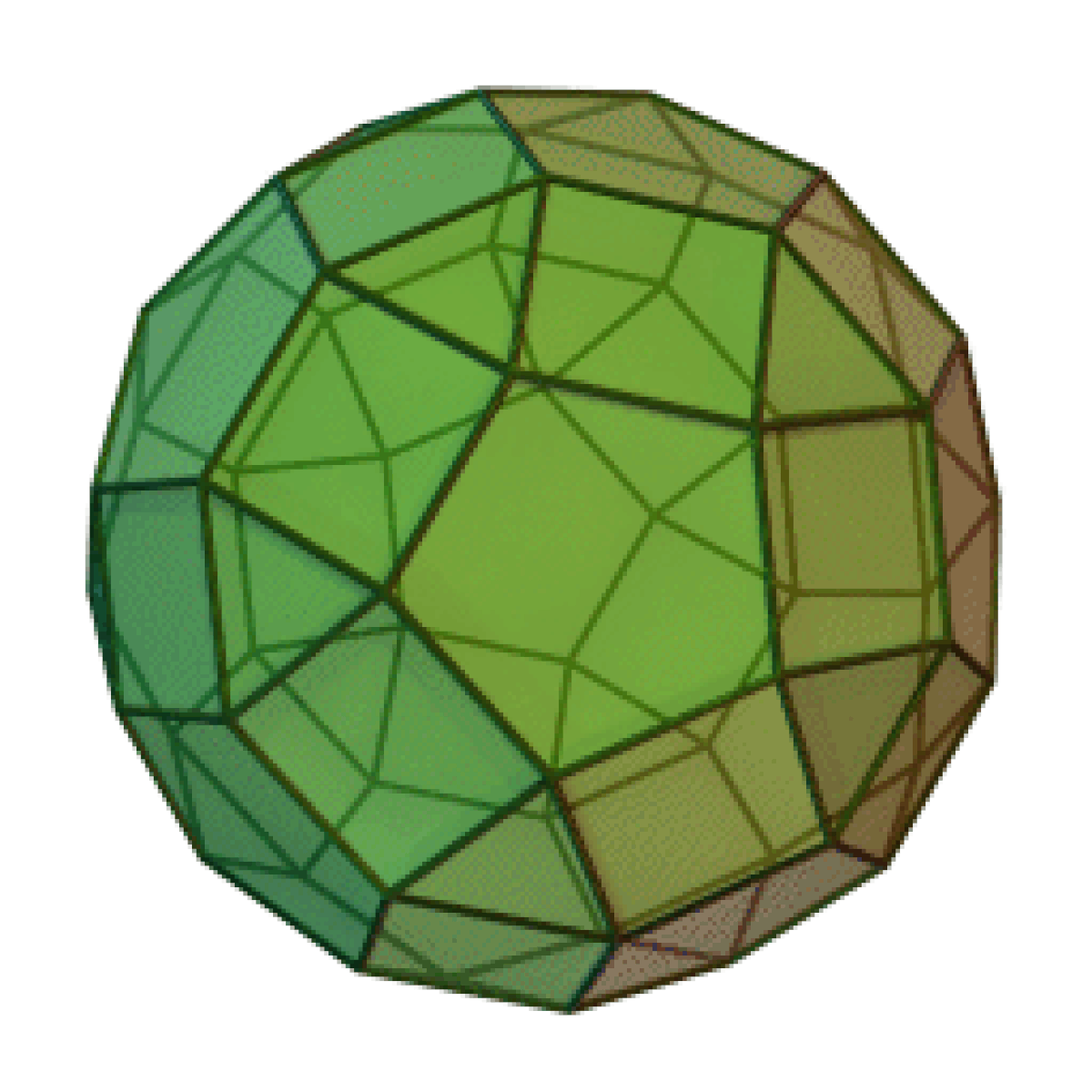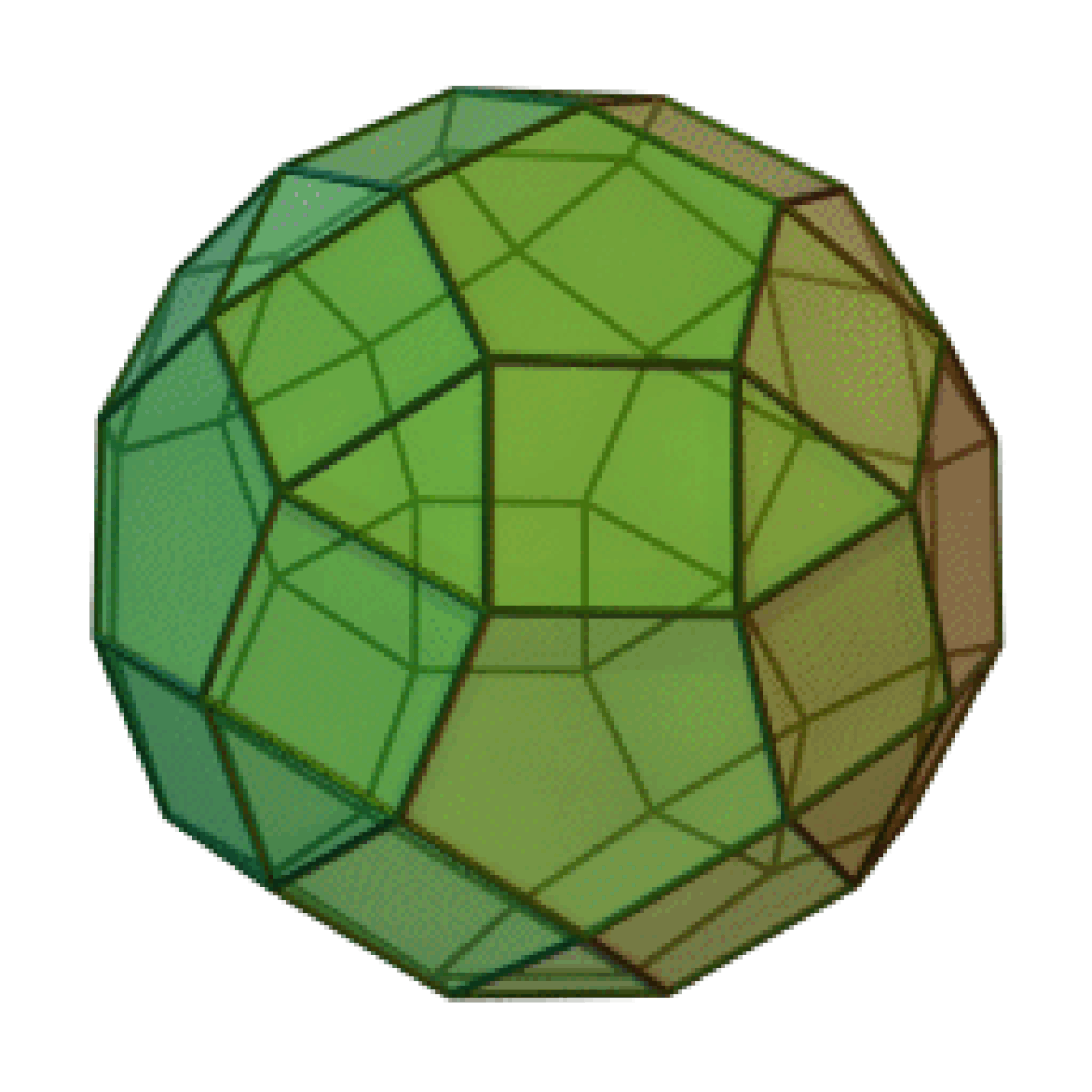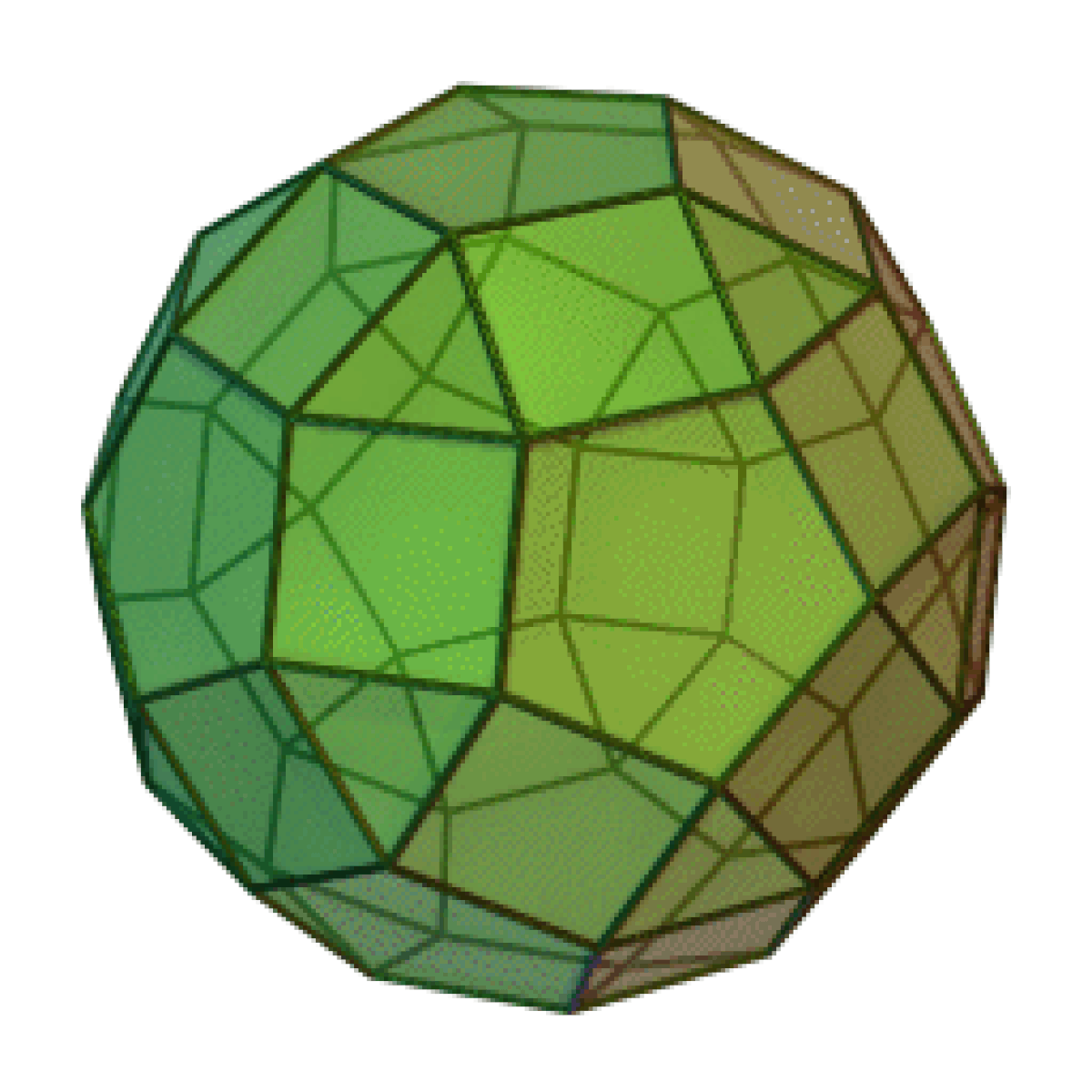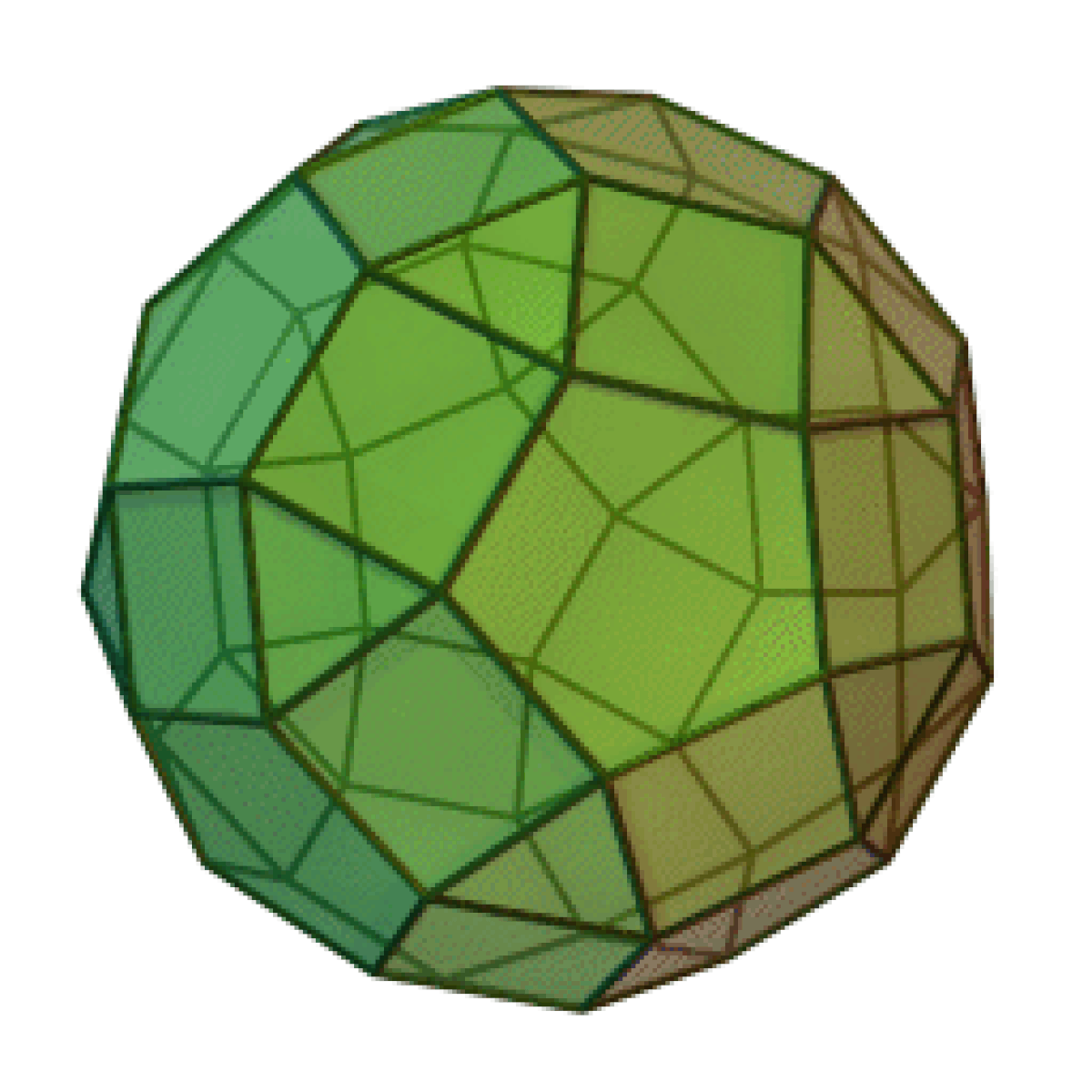
Le petit rhombicosidodécaèdre est un solide d'Archimède. Il possède 20 faces triangulaires régulières, 30 faces carrées régulières, 12 faces pentagonales régulières, 60 sommets et 120 arêtes.

Le nom rhombicosidodécaèdre fait référence au fait que les 30 faces carrées sont placées dans les mêmes plans que les 30 faces du triacontaèdre rhombique qui est le dual de l'icosidodécaèdre.

Il peut aussi être appelé un dodécaèdre étendu ou un icosaèdre étendu à partir des opérations de troncature du solide uniforme.

Relations géométriques

Si vous étendez un icosaèdre en déplaçant les faces de l'origine d'une certaine distance, sans changer l'orientation ou la taille des faces et que vous faites la même chose à son dual, le dodécaèdre et que vous remplissez les trous carrés dans le résultat, vous obtenez un petit rhombicosidodécaèdre. Par conséquent, il possède le même nombre de triangles qu'un icosaèdre et le même nombre de pentagones qu'un dodécaèdre, avec un carré pour chaque côté d'arête.

Les kits Zome pour fabriquer des dômes géodésiques et d'autres polyèdres utilisent des boules fendues comme connecteurs. Les boules sont des petits rhombicosidodécaèdres "développés", avec les carrés remplacés par des rectangles. Le développement est choisi de telle sorte que les rectangles résultants sont des rectangles d'or.

Coordonnées cartésiennes

Les coordonnées cartésiennes pour les sommets d'un petit rhombicosidodécaèdre centré à l'origine sont

,

,

,

,

,

,

,

,

,

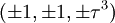
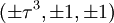
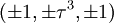
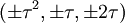
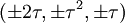
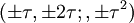
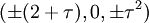
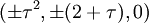
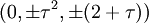
où est le nombre d'or.