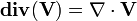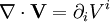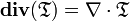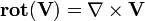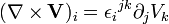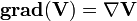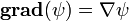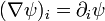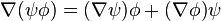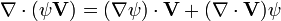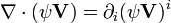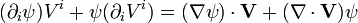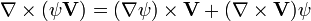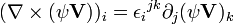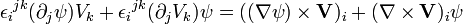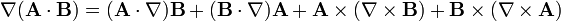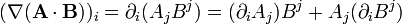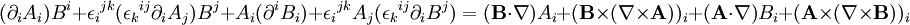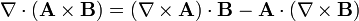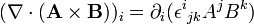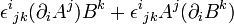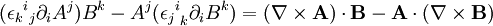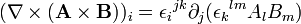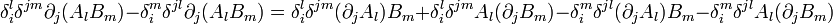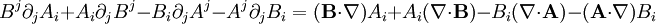Identités vectorielles - Définition
La liste des auteurs de cet article est disponible ici.
Opérateurs
Cette section fournit une liste explicite de la signification des symboles utilisés pour plus de clarté.
Divergence
Divergence d'un champ vectoriel
Pour un champ vectoriel
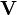
C'est un scalaire.
En convention de sommation d'Einstein la divergence d'un champ vectoriel s'écrit :
Divergence d'un tenseur
Pour un tenseur
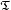
C'est un vecteur
Rotationnel
Pour un champ vectoriel
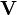
C'est un champ vectoriel.
En convention de sommation d'Einstein le rotationnel d'un champ vectoriel s'écrit :
Gradient
Gradient d'un champ vectoriel
Pour un champ vectoriel
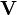
C'est un tenseur.
Gradient d'un champ scalaire
Pour un champ scalaire ψ, on écrit généralement le gradient comme suit :
C'est un vecteur.
En convention de sommation d'Einstein le gradient d'un champ scalaire s'écrit :
Autres identités impliquant des opérateurs
Dans cette section, ψ et φ représentent des champs scalaires,
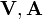
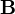
Cette relation découle immédiatement de la règle du produit.
En convention de sommation d'Einstein, on a :
La règle du produit étant d'application, ce dernier terme est équivalent à :
En convention de sommation d'Einstein, on a :
La règle du produit étant d'application, ce dernier terme est équivalent à :
En convention de sommation d'Einstein, on a :
Où la dernière égalité découle de la règle du produit. On peut décomposer ces deux termes en sous-termes :
En convention de sommation d'Einstein, on a :
La règle du produit étant d'application, ce dernier terme est équivalent à :
En effectuant une permutation paire d'indice sur le premier terme et une impaire sur le second, on obtient :
Le changement de signe provient de la permutation impaire d'indice du symbole de Levi-Civita.
L'identité est ainsi démontrée.En convention de sommation d'Einstein, on a :
En utilisant les propriétés du symbole de Levi-Civita ainsi que la règle du produit, on peut réécrire :
Le membre de droite peut être simplifié comme suit :