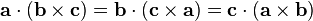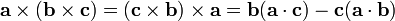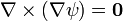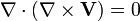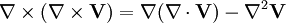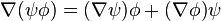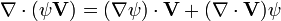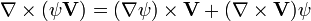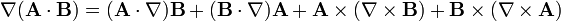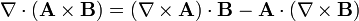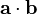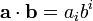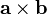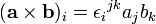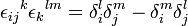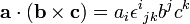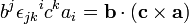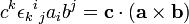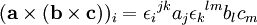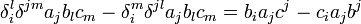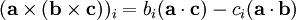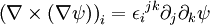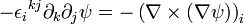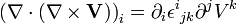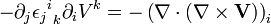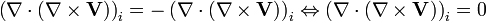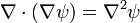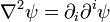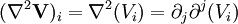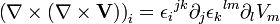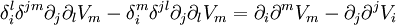Identités vectorielles - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Articles d'analyse vectorielle | |

| |
| Objets d'étude | |
| Champ vectoriel | Champ scalaire |
| Équation aux dérivées partielles | |
| de Laplace | de Poisson |
| Opérateurs | |
| Nabla | Gradient |
| Rotationnel | Divergence |
| Laplacien scalaire | Bilaplacien |
| Laplacien vectoriel | D'alembertien |
| Théorèmes | |
| de Green | de Stokes |
| de Helmholtz | de flux-divergence |
| du gradient | du rotationnel |
Les identités suivantes peuvent être utiles en analyse vectorielle.
Identités vectorielles générales
Dans cette section, a, b, c et d représentent des vecteurs quelconques.
Conventions d'écriture
Dans cet article, les conventions suivantes sont utilisées :
Produit scalaire
Le produit scalaire de deux vecteurs a et b est noté
En convention de sommation d'Einstein cela s'écrit :
Produit vectoriel
Le produit vectoriel de deux vecteurs a et b est noté
En convention de sommation d'Einstein cela s'écrit :
Symbole de Levi-Civita
Une identité revenant souvent dans les démonstrations utilisant la convention de sommation d'Einstein est la suivante :
Avec δ le symbole de Kronecker.
Triple produits
En convention de sommation d'Einstein on a :
En permutant deux fois les indices du symbole de Levi-Civita et en réarrangeant les termes on obtient tour à tour les expressions équivalentes suivantes :
Premièrement :
Deuxièmement :
La première égalité découle des propriétés du produit vectoriel :
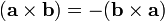
En convention de sommation d'Einstein on a :
En utilisant les propriétés du symbole de Levi-Civita et du symbole de Kronecker, le membre de droite peut se réécrire comme suit :
En explicitant le membre de droite on retrouve l'identité :
Autres Produits
En convention de sommation d'Einstein on a :
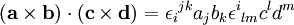
En utilisant les propriétés du symbole de Levi-Civita et du symbole de Kronecker, le membre de droite peut se réécrire comme suit :
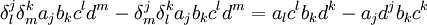
Le second membre étant obtenu en simplifiant et réarrangeant les termes. On retrouve dans ce membre de droite l'expression de produits scalaires et on a finalement :
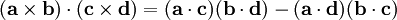
Combinaisons d'opérateurs
Rotationnel du gradient
Le rotationnel du gradient de n'importe quel champ scalaire ψ est toujours nul :
En convention de sommation d'Einstein on a :
En permutant les indices j et k (permutation impaire) on obtient l'expression équivalente :
Le changement de signe provient de la permutation impaire des indices. On a donc finalement :
Divergence du rotationnel
La divergence du rotationnel de n'importe quel champ vectoriel
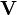
En convention de sommation d'Einstein on a :
En permutant les indices i et j (permutation impaire) on obtient l'expression équivalente :
Le changement de signe provient de la permutation impaire des indices. On a donc finalement :
Laplacien
Laplacien d'un champ scalaire
Le Laplacien d'un champ scalaire ψ est défini comme la divergence du gradient :
C'est un scalaire.
En convention de sommation d'Einstein, le Laplacien d'un champ scalaire se note comme suit :
Laplacien d'un champ vectoriel
Le Laplacien vectoriel d'un champ vectoriel est le vecteur dont les composantes sont les laplacien des composantes.
En convention de sommation d'Einstein cela se note :
Rotationnel du rotationnel
Le rotationnel du rotationnel d'un champ vectoriel
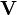
En convention de sommation d'Einstein on a :
En utilisant les propriétés du symbole de Levi-Civita et celles du symbole de Kronecker), on obtient alors :
On retrouve dans le membre de droite de cette dernière expression le gradient de la divergence et le Laplacien. On a donc finalement :