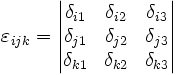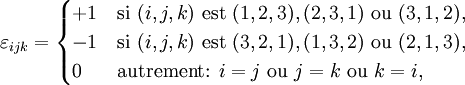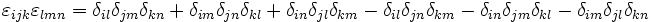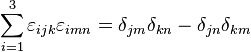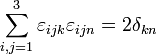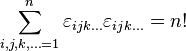Mercredi 30 Avril 2025
Rechercher 🔍
Mathématiques

Symbole de Levi-Civita - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs est disponible ici.

Le symbole de Levi-Civita, noté ε (lettre grecque epsilon), est un indicateur antisymétrique d'ordre 3 qui peut être exprimé à partir du symbole de Kronecker :

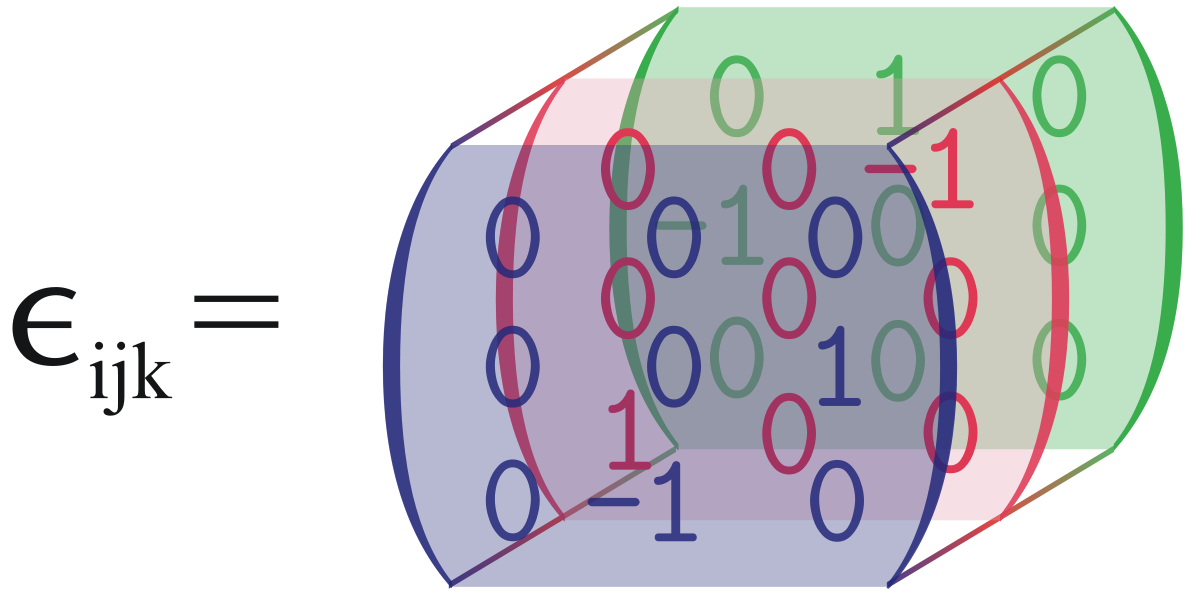
Visualisation d'un symbole de Levi-Civita en 3 dimensions.
Visualisation d'un symbole de Levi-Civita en 3 dimensions.
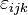
\varepsilon_{ijk} =\begin{vmatrix} \delta_{i1} & \delta_{i2}& \delta_{i3} \\ \delta_{j1} & \delta_{j2}& \delta_{j3} \\ \delta_{k1} & \delta_{k2}& \delta_{k3} \end{vmatrix}

Ainsi \varepsilon_{ijk} ne peut prendre que trois valeurs : -1, 0 ou 1.

En 3 dimensions on peut figurer le symbole de Levi-Civita comme suit :

\varepsilon_{ijk} = \begin{cases} +1 & \mbox{si } (i,j,k) \mbox{ est } (1,2,3), (2,3,1) \mbox{ ou } (3,1,2), \\ -1 & \mbox{si } (i,j,k) \mbox{ est } (3,2,1), (1,3,2) \mbox{ ou } (2,1,3), \\ 0 & \mbox{autrement: }i=j \mbox{ ou } j=k \mbox{ ou } k=i, \end{cases}

La relation du symbole Levi-Civita au symbole de Kronecker:

\varepsilon_{ijk}\varepsilon_{lmn} = \delta_{il}\delta_{jm}\delta_{kn} + \delta_{im}\delta_{jn}\delta_{kl} + \delta_{in}\delta_{jl}\delta_{km} - \delta_{il}\delta_{jn}\delta_{km} - \delta_{in}\delta_{jm}\delta_{kl} - \delta_{im}\delta_{jl}\delta_{kn}
\sum_{i=1}^3 \varepsilon_{ijk}\varepsilon_{imn} = \delta_{jm}\delta_{kn} - \delta_{jn}\delta_{km}
\sum_{i,j=1}^3 \varepsilon_{ijk}\varepsilon_{ijn} = 2\delta_{kn}

On peut démontrer que:

\sum_{i,j,k,\dots=1}^n \varepsilon_{ijk\dots}\varepsilon_{ijk\dots} = n!

est vrai en n dimensions.

miniature
Une gigantesque muraille de 10 milliards d'années-lumière dans l'Univers 🔭
miniature
Benchmark: les processeurs quantiques sous la loupe, quels sont les meilleurs ? 🏆
miniature
Découverte d'une "fourmi de l'enfer" vieille de 113 millions d'années 🐜
miniature
Le rôle méconnu de la décharge dans l'usure des batteries 🔋
miniature
La fonte des glaces déplace les pôles: quelles conséquences ? 🌍
miniature
L'appareil photo de votre smartphone peut détecter l'antimatière 📱
miniature
Cette étoile-zombie peut déformer les atomes à distance, et elle fonce dans notre galaxie ⭐
miniature
Un mosasaure géant découvert dans le Mississippi 🦕
miniature
Problème, les galaxies meurent plus tôt que prévu 🌀
miniature
Ce lien entre cannabis et troubles psychotiques 🧠
miniature
Une révolution dans le refroidissement des puces électroniques ? 🔥
miniature
Des parasites sous-marins filmés en train de vampiriser un poisson des abysses 👀
miniature
Lucy survole un astéroïde en forme de cacahuète 🚀
miniature
Découverte du fossile d'un dinosaure géant méconnu 🦕
miniature
Mars avait-elle un champ magnétique unilatéral ? 🔍
miniature
Des chimpanzés surpris à sociabiliser avec de l'alcool 🍇
miniature
Découverte macabre: ce gladiateur a été tué par un lion il y a 1 800 ans... en Grande-Bretagne 🦁
miniature
L'électroluminescence du graphène, une découverte inattendue ! 💡
miniature
Cet objet métallique n'a pas été fabriqué sur Terre 🔧
miniature
1
Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡
miniature
Cette super-Terre brûle les attentes des astronomes 🔥
miniature
Découverte exceptionnelle de fossiles d'amphibiens géants 🐸
miniature
Voici ce qui a causé les toutes premières inégalités de richesse 💰
miniature
Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊
miniature
Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭
miniature
Des cellules solaires flexibles battent des records d'efficacité ⚡
miniature
Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀
miniature
Record établi pour un transistor en diamant 💎
miniature
Les sursauts radio rapides trahissent enfin leur origine cosmique 📡
miniature
Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠
miniature
Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊
miniature
Les oscillations collectives des foules humaines denses 🔁
miniature
Une forme inconnue de la matière détectée au LHC ? ⚛️
miniature
Le sel, un facteur méconnu de l'obésité ? 🧂
miniature
L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀
miniature
Découverte tectonique majeure sous les Petites Antilles 🌍
miniature
1
Peut-on geler en chauffant ? ❄️
miniature
Une peau électronique pour doter les robots du sens du toucher 👌
miniature
Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳
miniature
Le cancer inscrit dans nos gènes dès la naissance ? 🧬
miniature
Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥
miniature
Le passé verdoyant du plus grand désert du monde 🐪
miniature
Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷
miniature
Des puces quantiques plus proches que jamais ⚡
miniature
1
Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬
miniature
En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊
miniature
Des scientifiques parviennent à produire efficacement du carburant à partir de monoxyde de carbone 🛢️
miniature
Que nous apprend la découverte de cet insecte de 16 millions d'années ? 🐜
miniature
Avec 91km, l'accélérateur FCC fera passer le LHC pour un jouet ⚛️
miniature
Cette vitamine développe les fonctions cognitives du cerveau 🧠
Page générée en 0.068 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise