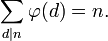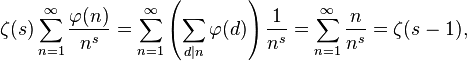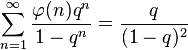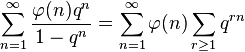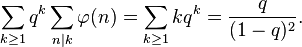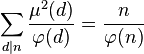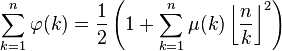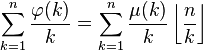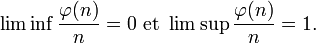Indicatrice d'Euler - Définition

Autres propriétés

Arithmétique modulaire

L'indicatrice d'Euler est une fonction essentielle de l'arithmétique modulaire, elle est à la base de résultats fondamentaux, à la fois en mathématiques pures et appliquées.

• Un entier p est premier si et seulement si φ(p) = p - 1.

Cette propriété est une conséquence directe du calcul explicite de l'indicatrice.

La cryptologie utilise largement cette fonction. Le code RSA se fonde sur le théorème d'Euler, indiquant que si n est un entier strictement positif et a un entier premier avec n, alors a^φ(n) ≡ 1 (mod n).

Une autre branche de la théorie de l'information utilise l'indicatrice : la théorie des codes. C'est les cas des codes correcteurs, et particulièrement des codes cycliques. Ce type de code se construit à l'aide de polynôme cyclotomique et le degré du polynôme cyclotomique Φ_n d'indice n à coefficients dans les entiers est égal à φ(n). Plus précisément, on dispose des égalités suivantes :

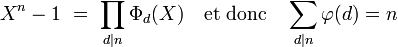
La somme et le produit sont étendus à tous les diviseurs positifs d de n.

La formule d'inversion de Möbius permet d'inverser cette somme :

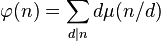
Ici, μ désigne la fonction de Möbius usuelle définie sur l'ensemble des entiers strictement positifs, la démonstration est proposée dans l'article associé.

Théorie analytique des nombres

Les deux fonctions génératices présentées ici sont des conséquences directes du fait que :

Une série de Dirichlet utilisant est

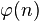
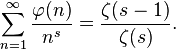
qui est dérivé depuis :

ou ζ(s) est la Fonction zêta de Riemann.

Une série de Lambert utilisant est

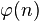
qui converge pour |q|<1.

dérivé de :

avec

Autres formules impliquant la fonction φ d'Euler

pour

pour

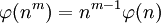
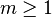
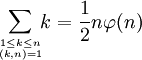
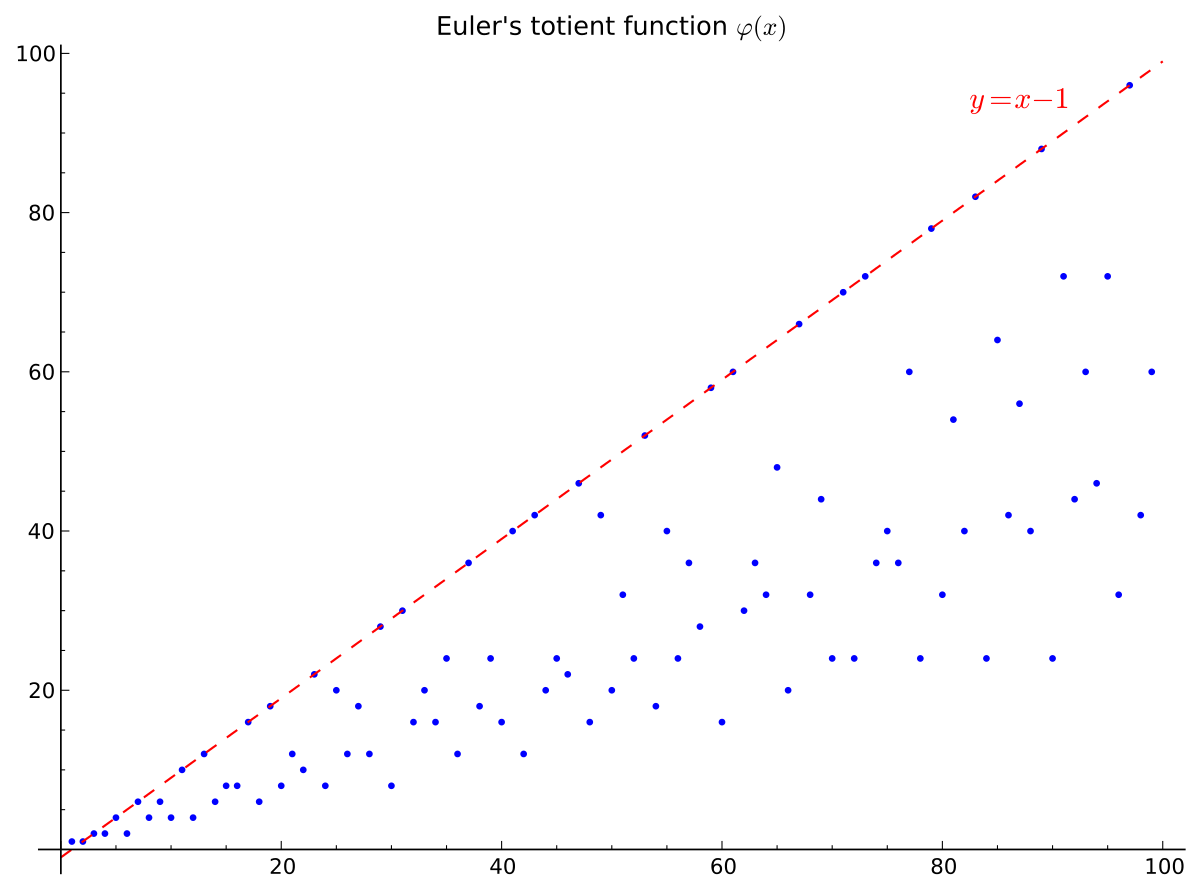
Les 99 premières valeurs de la fonction φ

	+0	+1	+2	+3	+4	+5	+6	+7	+8	+9
0+		1	1	2	2	4	2	6	4	6
10+	4	10	4	12	6	8	8	16	6	18
20+	8	12	10	22	8	20	12	18	12	28
30+	8	30	16	20	16	24	12	36	18	24
40+	16	40	12	42	20	24	22	46	16	42
50+	20	32	24	52	18	40	24	36	28	58
60+	16	60	30	36	32	48	20	66	32	44
70+	24	70	24	72	36	40	36	60	24	78
80+	32	54	40	82	24	64	42	56	40	88
90+	24	72	44	60	46	72	32	96	42	60

Conjectures

• n est premier si et seulement si (énoncée par Derrick Henry Lehmer)
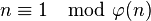
• (énoncée par Robert Daniel Carmichael)

Inégalités

Certaines inégalités impliquant la fonction sont :

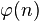
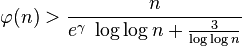pour n > 2, où est la constante d'Euler,

pour n > 0,

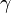
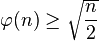
et

pour n > 6.

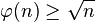
Pour un nombre premier n, clairement . Pour un nombre composé n, nous avons

(pour un nombre composé n).

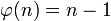
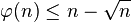
Pour tous les n > 1 :

Pour un grand n aléatoire, ces bornes ne peuvent pas être encore améliorées, ou être plus précises :

Une paire d'inégalités combinant la fonction et la fonction diviseur σ sont :