Fonction de Möbius - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, la fonction de Möbius désigne généralement une fonction multiplicative particulière, définie sur les entiers positifs et à valeurs dans l'ensemble {-1, 0, 1}.
Elle est utilisée dans des branches différentes des mathématiques. Vue sous un angle élémentaire, la fonction de Möbius permet certains calculs de dénombrement, en particulier pour l'étude des p-groupes ou en théorie des graphes. En arithmétique, elle est parfois définie comme l'inverse de la fonction multiplicative constante 1, pour l'opération convolution de Dirichlet. On la trouve encore pour l'étude des polynômes cyclotomiques sur le corps des nombres rationnels. Son rôle est analogue pour les corps finis et, par voie de conséquence la fonction de Möbius intervient dans la théorie des codes correcteurs. En théorie analytique des nombres, la fonction de Möbius est plus souvent introduite à l'aide des séries de Dirichlet. Elle intervient dans certaines démonstrations liées à l'étude de l'hypothèse de Riemann sur les nombres premiers.
L'usage de cette fonction est ancien en mathématiques, on le trouve chez Leonhard Euler en 1748 ou encore chez Gauss dans son livre Disquisitiones arithmeticae en 1801. C'est néanmoins Möbius qui le premier l'étudie systématiquement en 1832.
Définition et propriétés
Définition
Dans toute la suite de l'article N désigne l'ensemble des entiers positifs et N* celui des entiers strictement positifs. La définition la plus courante est la suivante :
Définition de la fonction de Möbius — La fonction de Möbius est définie de N* dans {-1, 0, 1}. Si n est un nombre entier, son image par la fonction est généralement noté μ(n), elle est nulle si n est divisible par un carré parfait différent de 1, vaut 1 si n est le produit d'un nombre pair de nombres premiers distincts et -1 sinon.
Un rapide calcul montre que les premières valeurs de la fonction de Möbius sont :
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| μ(n) | 1 | -1 | -1 | 0 | -1 | 1 | -1 | 0 | 0 | 1 | -1 | 0 | -1 | 1 | 1 | 0 | -1 | 0 | -1 | 0 |
Le calcul des cinquante premières valeurs donne le graphe :
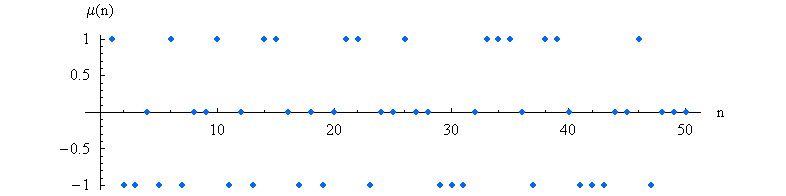
Fonction multiplicative
La fonction de Möbius est multiplicative, ce qui signifie que :
Fonction multiplicative — L'image par μ de 1 est égale à 1, et si n et m deux entiers strictement positifs premiers entre eux, on dispose de l'égalité :
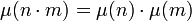
En effet, si l'un des deux entiers n et m est divisible par un carré parfait différent de 1, la formule est vérifiée et donne 0. Sinon, soit s le nombre de diviseurs premiers de n et t celui de m. L'entier n.m admet s + t diviseurs premiers. L'égalité suivante démontre le théorème :
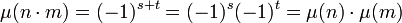
Formule d'inversion de Möbius
Le fait que la fonction de Möbius soit multiplicative est lourd de conséquences. Elle est un élément clé du résultat suivant :
Théorème 1 — La somme des valeurs de la fonction de Möbius sur tous les diviseurs positifs de n est nulle, si n est un entier strictement supérieur à 1. Plus précisément :

Ce résultat est parfois vu comme une étape intermédiaire de la formule suivante :
Formule d'inversion de Möbius — Soient f une fonction arithmétique et g la fonction définie par :
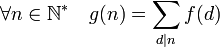
La fonction g vérifie l'égalité :
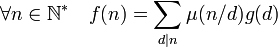
La fonction f peut être vue comme une suite, à valeurs dans les entiers ou plus généralement dans les nombres complexes. Le résultat est encore vrai si f est à valeurs dans un groupe additif quelconque.
Si d est égal à 1, le résultat est évident. Sinon, soit P = {p1,..., ps} l'ensemble des nombres premiers diviseurs de d. Les diviseurs de d sont tous des produits de puissances d'éléments de P. Si au moins une de ces puissances est strictement supérieure à 1, ces diviseurs ont pour image par la fonction de Möbius la valeur 0. Ce qui revient à dire que l'on peut ne considérer que les produits dont les facteurs sont des éléments de P tous distincts et :
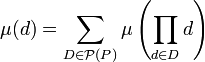
Ici, P(P) désigne l'ensemble des parties de P. Par définition de la fonction μ, on dispose encore de l'égalité, si Card (D) désigne le cardinal de D :
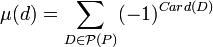
Dans un ensemble à s éléments, le nombre de sous-ensembles à t éléments, où t est un entier plus petit que s, et donnée par le coefficient binomial ce qui permet encore d'écrire, avec les notations usuelles :
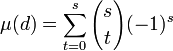
La formule du binôme montre que :
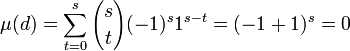
Cette dernière égalité termine la démonstration du théorème.
-
- Démonstration alternative :
La démonstration précédente revient à montrer qu'il existe autant de sous-ensembles dans P ayant un nombre pair d'élément que de sous-ensemble ayant un cardinal impair. Pour s'en persuader, on regroupe tous les sous-ensembles de P en paire. Soit p un élément de P, le premier élément d'une paire quelconque est un sous-ensemble S de P ne contenant pas p et le deuxième est l'union de S et de p. Les paires sont disjointes deux à deux et leur union est égale à P. Chaque paire contient un ensemble de cardinal pair et un de cardinal impair. Ce qui montre bien qu'il existe autant de sous-ensembles pairs et impairs dans P.


















































