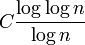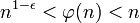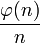Indicatrice d'Euler - Définition

Introduction

Les mille premières valeurs de φ(n)

En mathématiques, l'indicatrice d'Euler est une fonction de la théorie des nombres.

Elle est utilisée pour les mathématiques pures, à la fois en théorie des groupes, en théorie algébrique des nombres et en théorie analytique des nombres.

En mathématiques appliquées, à travers l'arithmétique modulaire, elle joue un rôle important en théorie de l'information et plus particulièrement en cryptologie.

La fonction indicatrice est aussi appelée fonction phi d'Euler ou simplement la fonction phi, car la lettre φ est communément utilisée pour la désigner.

Elle est nommée en l'honneur du mathématicien suisse Leonhard Euler qui fut le premier à l'étudier.

Définition et calcul explicite

Définition et exemple

• L'indicatrice d'Euler φ est la fonction de l'ensemble des entiers strictement positifs dans lui-même, qui à n associe le nombre d'entiers positifs inférieurs à n et premiers avec n.

Par exemple, φ(8) = 4 car les quatre nombres 1, 3, 5 et 7 sont premiers avec 8. Par ailleurs φ(1)=1 - c'est le seul nombre qui est égal à son indicatrice d'Euler.

Premières propriétés

Dans ce paragraphe, n désigne un entier strictement positif.

• La valeur φ(n) est égale au nombre d'éléments primitifs d'un groupe cyclique d'ordre n.

Un élément primitif désigne un membre du groupe engendrant le groupe entier. Cette propriété est démontrée dans le paragraphe Théorème fondamental de l'article Groupe cyclique.

• La valeur φ(n) est égale à l'ordre du groupe des unités de l'anneau Z/nZ.

Le groupe des unités désigne l'ensemble des éléments inversibles pour la multiplication de l'anneau. Cette propriété est démontrée dans le paragraphe Groupe des unités de l'article Anneau Z/nZ.

• Si u et v sont deux entiers strictement positifs et premiers entre eux, alors φ(u.v)=φ(u).φ(v).

Une telle fonction est dite multiplicative. Cette propriété est une conséquence du théorème des restes chinois. En effet, soit G d'ordre u.v, et G_u et G_v d'ordres respectifs u et v. Le théorème chinois montre que G est isomorphe à G_uxG_v. Un élément du groupe produit est générateur si et seulement si sa première composante est génératrice du premier groupe et sa deuxième composante est génératrice du deuxième groupe. Le nombre d'éléments générateurs du groupe produit est donc égal à φ(u).φ(v). L'isomorphisme montre que cette valeur est égale au nombre d'éléments générateurs du groupe G, ce qui démontre la formule recherchée.

Calcul

La valeur de l'indicatrice d'Euler s'obtient par l'expression de n donnée par le théorème fondamental de l'arithmétique :

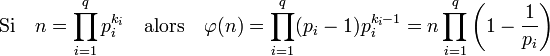
Dans la formule, p_i désigne un nombre premier et k_i un entier strictement positif.

En effet, le caractère multiplicatif de l'indicatrice d'Euler et une récurrence montrent que :

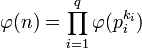
Il suffit alors de dénombrer le nombre d'entiers non premiers avec une puissance d'un nombre premier et plus petit que celui-ci pour remarquer que :

Ce qui permet de conclure la démonstration.

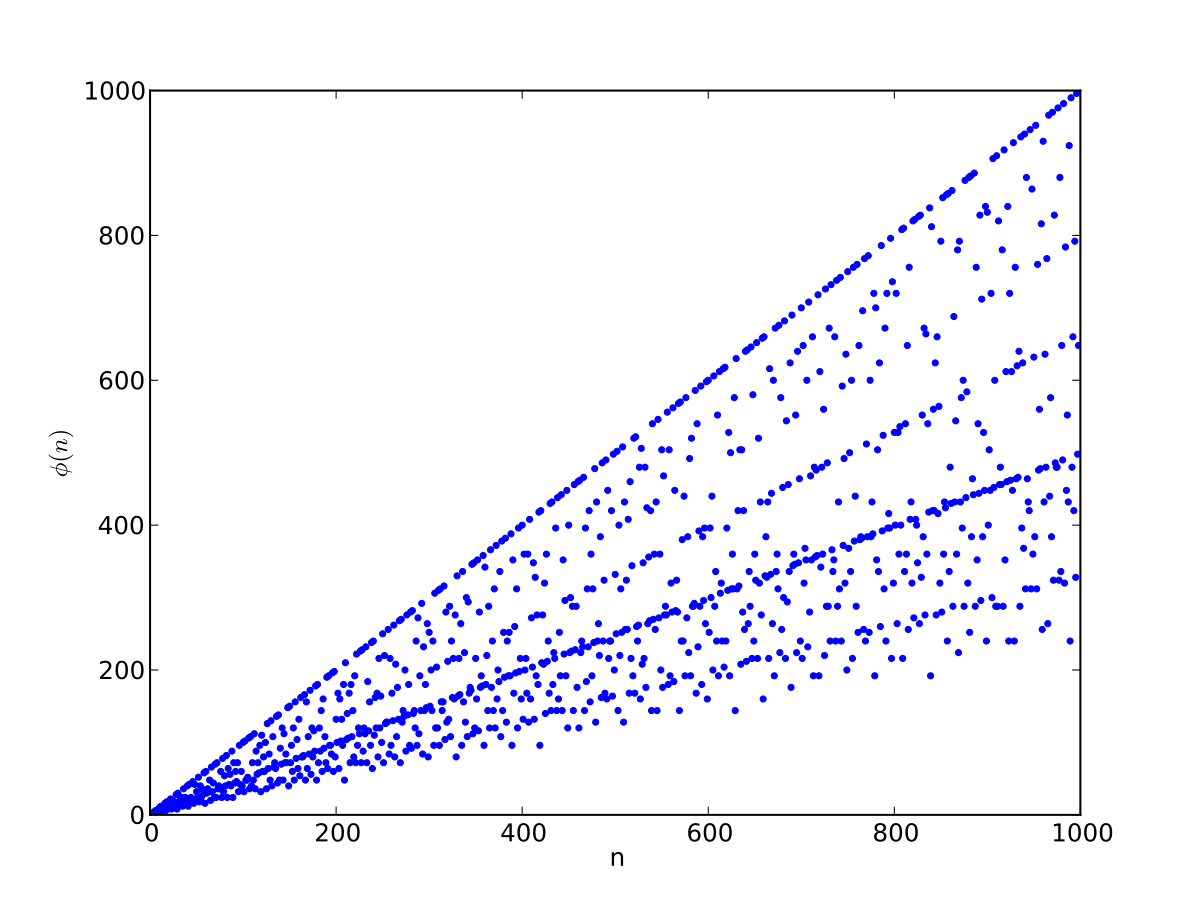
Croissance de la fonction

La croissance de comme une fonction de n est une question intéressante. La première impression que l'on a pour les petits n est que doit être notablement plus petit que n est quelque peu erronée. Asymptotiquement, nous avons

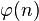
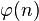
pour n'importe quel et . En fait, si nous considérons

nous pouvons écrire, à partir de la formule précédente, sous forme de produit de facteurs

où les p sont des nombres premiers divisant n. Par conséquent les valeurs de n correspondantes aux valeurs particulièrement petites du rapport sont les n qui sont le produit d'un segment initial de la suite de tous les nombres premiers. À partir du théorème des nombres premiers il peut être montré qu'une constante ε dans la formule précédente peut par conséquent être remplacée par

.