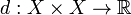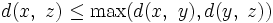Métrique (mathématiques) - Définition

Introduction

En mathématiques, une métrique ou fonction distance est une fonction qui définit une distance entre les éléments d'un ensemble. Un ensemble avec une métrique est appelé un espace métrique. Une métrique induit une topologie sur un ensemble mais toutes les topologies ne sont pas engendrées par une métrique.

En géométrie différentielle, le mot "métrique" est aussi utilisé pour faire référence à une structure définie seulement sur un espace vectoriel qui est plus proprement qualifié un tenseur métrique (ou riemannien ou métrique pseudo-riemannienne).

Définition

Une métrique sur un ensemble X est une fonction (appelée la fonction distance ou simplement distance)

(où est l'ensemble des nombres réels). Pour tout x, y, z dans X, cette fonction doit satisfaire les conditions suivantes :

1. (non-négativité)
2. si et seulement si (identité des indiscernables)
3. (symétrie)
4. (inégalité triangulaire).

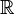
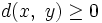
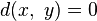
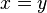
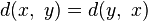
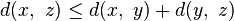
Une métrique d sur X est appelée intrinsèque si deux points quelconques x et y dans X peuvent être joints par une courbe de longueur arbitrairement proche de d(x, y).

Pour les ensembles où une addition est définie, nous appelons d une métrique invariante par translation si

quels que soient x,y et a dans X.

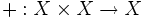
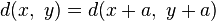
Si l'inégalité triangulaire est renforcée par

la métrique est appelée ultramétrique, voir ci-dessous.