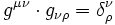Tenseur métrique - Définition

Introduction

En géométrie et plus particulièrement en géométrie différentielle, le tenseur métrique est un tenseur de rang 2 qui est utilisé pour la mesure des distances et des angles. Il généralise le théorème de Pythagore. Dans un système de coordonnées donné, le tenseur métrique peut se représenter comme une matrice, généralement notée G. Dans ce qui suit, la convention de sommation d'Einstein est utilisée.

Définition

Le tenseur métrique est un tenseur de rang 2 (c'est-à-dire une forme bilinéaire) défini sur un espace vectoriel E de dimension finie:

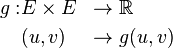
g est :

• symétrique :
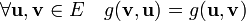
• non dégénérée :
• définie positive: (exception pour les pseudo-métriques, voir ci-dessous)

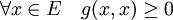
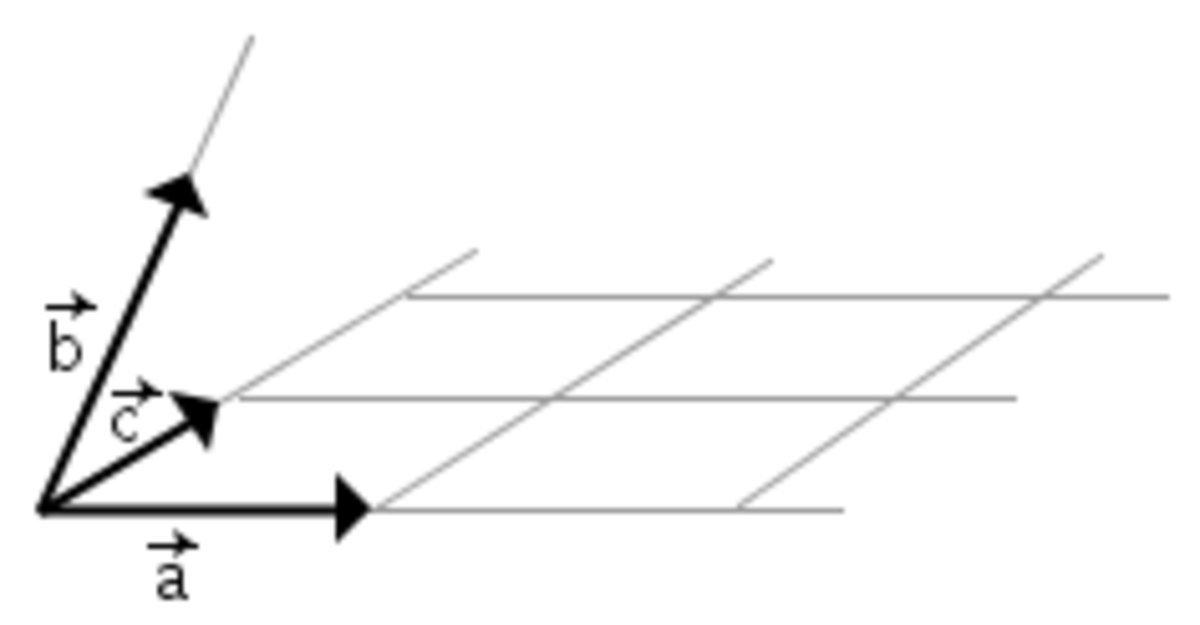
On note le produit scalaire de 2 vecteurs uⁱe_i et v^je_j de la manière suivante:

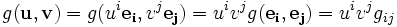
La notation g_ij est conventionnellement utilisée pour les composantes du tenseur métrique.

Coordonnées rectilignes

Nous supposons ici une base quelconque, , Le tenseur métrique se calcule alors simplement:

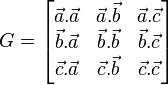
où désigne le produit scalaire de et de exprimé dans un repère orthonormé cartésien.

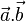
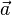
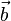
Pseudo-métrique

Lorsque g(x,x) n'est pas toujours positif, on peut parler de pseudo-métrique, c'est par exemple le cas de l'espace de Minkowski. Dans ce cadre, le produit scalaire g(x,x) (que l'on note η(x,x)) représente la pseudo-norme au carré. On note s la distance minkowskienne entre deux points P₁ et P₂ définie par:

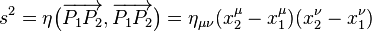
avec, pour l'espace de Minkowski, comme matrice du produit scalaire :

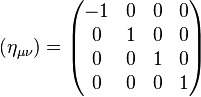
et ds² la distance minkowskienne au carré entre deux points infiniment voisins :

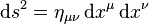
Pour un vecteur x d'un tel espace, nous avons les définitions suivantes :

Une courbe de cet espace-temps décrite par l'équation (x⁰(τ),x¹(τ),x²(τ),x³(τ)) où τ est un paramètre, admet comme vecteur tangent dx^μ / dτ. Le signe de la pseudo-norme de ce vecteur est idépendant du choix de τ et nous avons les définitions suivantes (cf. relativité restreinte) :

Montée et descente d'indices

Le tenseur métrique sert à monter ou à descendre les indices des coordonnées de vecteurs / formes différentielles / tenseurs. Prenons le cas du vecteur . Les produits correspondent à la forme linéaire , un élément de l'espace dual, qui à un vecteur associe le réel . Ils la définissent à travers ses coordonnées dans la base duale: où désignent les vecteurs de la base duale. Autrement dit le tenseur métrique a abaissé la position des indices de x^α en x_β transformant le vecteur en le covecteur .

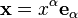
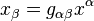
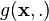
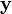
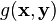
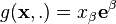
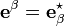
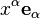
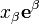
Cas des coordonnées curvilignes

Coordonnées curvilignes

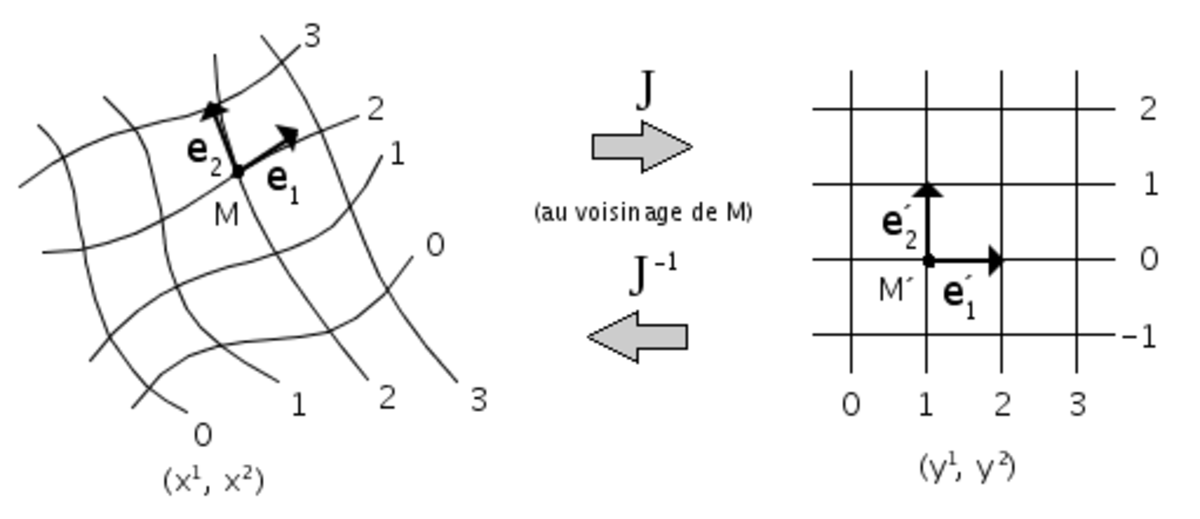
Lorsqu'il s'agit d'un système de coordonnées curvilignes, nous ne pouvons pas définir de base à ce repère à proprement parler. Les vecteurs de cette base e_i varient en fonction des coordonnées xⁱ d'un point. Il n'est donc pas possible de calculer un tenseur métrique constant. Cependant la matrice jacobienne J fournit une approximation linéaire de ce type de transformation au voisinage d'un point, la base locale, (e₁,e₂), étant simplement les vecteurs tangents aux axes de coordonnées. Il suffit donc de calculer les n² produits scalaires possibles de ces vecteurs tangents (composantes contravariantes de la jacobienne) pour obtenir le tenseur métrique G. Ceci revient à calculer J^TJ.

G devient alors un champ tensoriel. Le « champ de base » ainsi utilisé repère des vecteurs infinitésimaux, ceci se traduisant par un « produit scalaire infinitésimal ». On adopte alors l'écriture suivante: ds² = g_ijdxⁱdx^j (où ds désigne la variation de la norme et non pas celle du produit scalaire comme on pourrait le penser). La quantité s est aussi appelé abscisse curviligne.

Détails de calcul

Pour calculer le tenseur métrique à partir des équations donnant la relation entre l'espace considéré et un espace cartésien, c'est-à-dire un espace pour lequel g_ij = δ_ij (cfr. delta de Kronecker), il faut calculer la matrice jacobienne de ces équations. Le tenseur métrique est le produit de sa transposée par elle-même:

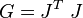
En appliquant la même opération à partir des équations donnant la relation entre l'espace cartésien et l'espace considéré, on obtient alors l'expression contravariante du tenseur. On peut alors retrouver son expression covariante en sachant que , où g^μν est l'expression contravariante du tenseur, et g_νρ son expression covariante.