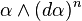Géométrie différentielle - Définition

Introduction

En mathématique, la géométrie différentielle est l'application des outils du calcul différentiel à l'étude de la géométrie. Les objets d'étude de base sont les variétés différentielles, ensembles ayant une régularité suffisante pour envisager la notion de dérivation, et les fonctions définies sur ces variétés.

La géométrie différentielle trouve sa principale application physique dans la théorie de la relativité où elle permet une modélisation d'une courbure de l'espace-temps. On peut également citer d'autres applications en physique classique. En mécanique des milieux continus par exemple, elle est utile à la description des déformations des corps élastiques, en particulier des poutres ou des coques. Un théorème comme celui de la boule chevelue s'applique à des situations aussi diverses que la géométrie d'un tokamak ou la nécessité de systèmes cycloniques ou anticycloniques en météorologie.

Points de vue intrinsèque et extrinsèque

Jusqu'au milieu du XIX^e siècle, la géométrie différentielle avait essentiellement un point de vue extrinsèque au sujet des variétés rencontrées, ce qui signifie que celles-ci étaient définies comme un sous-ensemble d'un espace vectoriel topologique (le plus souvent de dimension finie). Par exemple, on étudiait les propriétés d'une courbe pour donner un sens aux notions de tangence, de courbure, etc.

Le point de vue intrinsèque a l'avantage d'être bien plus flexible que le point de vue extrinsèque, ne serait-ce que parce qu'il ne force pas à trouver un espace pouvant « contenir » la variété considérée, ce qui peut parfois se révéler difficile. Par exemple la bouteille de Klein est une surface (c'est-à-dire une variété de dimension 2) mais pour la plonger dans un espace ambiant il faut choisir . De même, il n'est pas évident de trouver un espace « contenant » l'espace-temps courbé. Cependant, la flexibilité gagnée se traduit en une abstraction et une difficulté accrues pour définir les notions géométriques comme la courbure ou topologiques comme la connexité.

Branches de la géométrie différentielle

Géométrie riemannienne

La géométrie riemannienne est l'étude des métriques riemaniennes : une telle métrique est une famille de produits euclidiens sur une variété différentielle. Cette structure supplémentaire fait apparaître la variété comme un espace euclidien selon un point de vue infinitésimal. Elle permet de généraliser les notions de longueur de la courbe et de mesure de Lebesgue, l'analyse du gradient d'une fonction, de la divergence, etc. Son fort développement durant la seconde moitié du XX^e siècle s'explique par l'intérêt que lui ont porté aussi bien les géomètres que les analystes ou les physiciens. De plus, les métriques riemanniennes peuvent être arbitrairement introduites pour mener à bien les calculs sur les variétés.

Géométrie de Finsler

La géométrie de Finsler est une extension de la géométrie riemannienne, qui prend tout son sens en dimension infinie (par exemple pour l'étude des groupes de difféomorphismes sur une variété). Le principal objet d'étude est la variété de Finsler, id est une variété différentielle munie d'une métrique de Finsler, une norme de Banach définie sur chaque espace tangent.

Géométrie symplectique

La géométrie symplectique est l'étude des formes symplectiques, i.e. des « formes différentielles fermées non dégénérées ». Ces objets ont été introduits dans l'optique d'une formulation mathématique de la mécanique classique. Si les motivations physiques remontent à Lagrange et Hamilton, la géométrie symplectique s'est formée comme domaine d'études à part entière depuis les années 1960 et est aujourd'hui devenu un domaine actif de recherche. Contrairement à la géométrie riemannienne, des questions d'existence des structures se posent. Les principaux moteurs de recherche sont la conjecture d'Arnold, la conjecture de Weinstein et la quantification.

Géométrie de contact

La géométrie de contact est la sœur de la géométrie symplectique en dimension impaire. Il s'agit essentiellement de l'étude des formes de contact, c'est-à-dire des 1-formes différentielles α telles que soit une forme volume (ne s'annule en aucun point). Même si a priori l'objet d'étude semble différent, « sœur » est une dénomination doublement justifiée. D'une part car les géométries symplectique et de contact présentent des résultats « élémentaires » analogues. D'autre part, car des hypersurfaces présentant des structures de contact sont omniprésentes en géométrie symplectique.