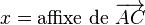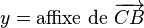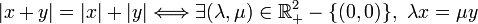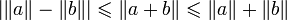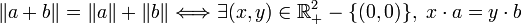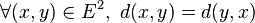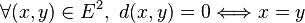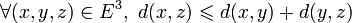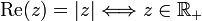Inégalité triangulaire - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, l'inégalité triangulaire exprime en substance que le chemin direct est le plus court. Cette inégalité peut être énoncée sous la forme d'une propriété ou bien d'une condition nécessaire à la bonne définition d'une distance.
Énoncés
En géométrie
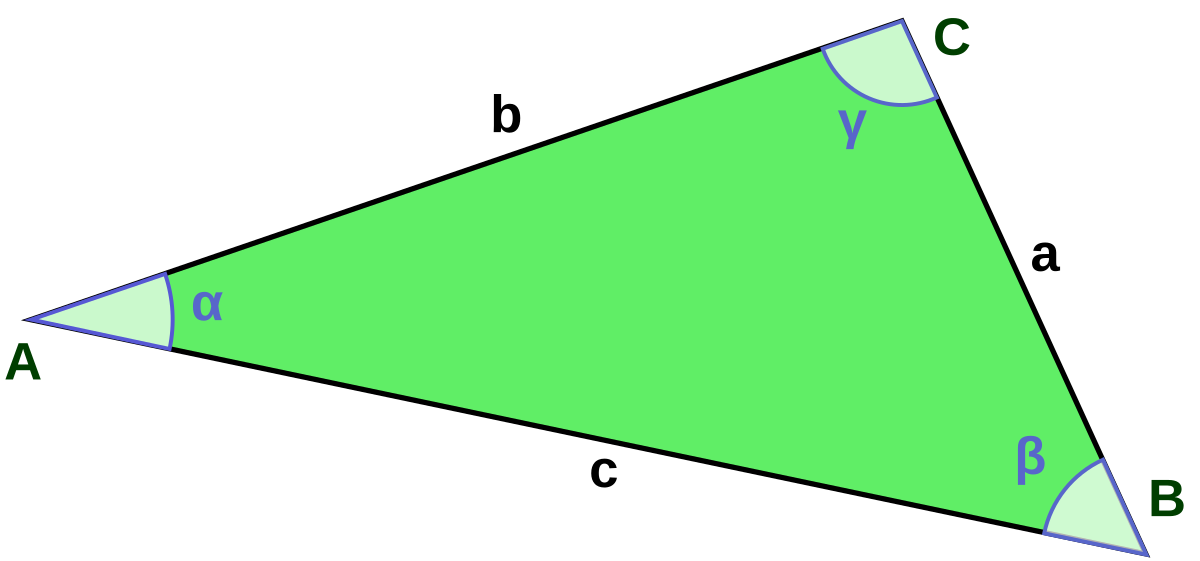
Dans un plan euclidien, soit un triangle ABC. Alors les longueur AB, AC et CB vérifient les 3 inégalités suivantes :
Deux propriétés complètent cette inégalité :
Pour les nombres complexes
En utilisant une représentation complexe du plan euclidien, on peut noter
On obtient cette formulation équivalente.
Pour
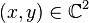
Généralisation aux espaces préhilbertiens
Soit
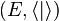

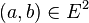
Point de vue axiomatique
Voir Distance (mathématiques) pour un article plus détaillé sur la notion de distance en mathématiques.
Soit E un ensemble et
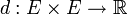
La troisième propriété demandée à d pour être une distance est de vérifier l'inégalité triangulaire.
Démonstrations
Lemme
Enoncé
Pour
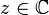
Démonstration
Soient
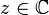
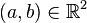
Premièrement,
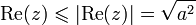
Ensuite,
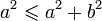
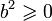
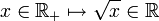
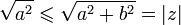
Finalement
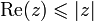
Il y a égalité si Re(z) = | Re(z) | , c'est-à-dire si a est positif, et si | Re(z) | 2 = | z | 2, c'est-à-dire si b = 0.
Dans le cadre des nombres complexes
Soit
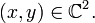
Inégalités
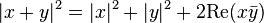
Or
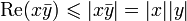
Donc
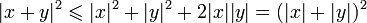
Par croissance de
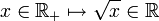
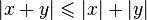
Posons x' = − x et y' = x + y.
Par ce qui précède, on a
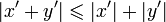
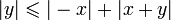
Donc
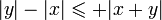
De même,
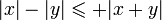
Finalement,
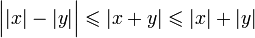
Cas d'égalité
Supposons que | x + y | = | x | + | y | .
On a alors
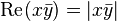
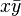
Donc
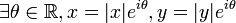
Finalement, on a bien λx = μy, avec λ = | y | et μ = | x | m.
Dans le cadre d'un plan euclidien
La démonstration la plus rapide est d'utiliser une représentation complexe du plan euclidien et d'appliquer le résultat précédemment démontré.
Dans le cadre des espaces préhilbertiens
La démonstration a exactement la même structure que pour les complexes.
Soit
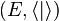
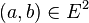
Inégalités
On a
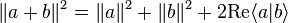
Par le lemme,
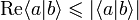
Par l'inégalité de Cauchy-Schwarz,
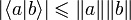
D'où
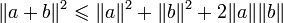
Et donc
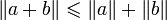
Posons a' = − a et b' = b + a. On a, par ce qui précède,
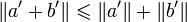
C'est-à-dire, comme
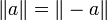
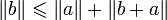
En faisant de même en intervertissant a et b, on obtient
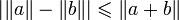
Finalement,
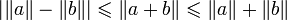
Cas d'égalité
Supposons que
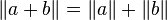
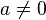
Par ce qui précède, on a donc
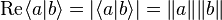
Donc, par le cas d'égalité de Cauchy-Schwarz,
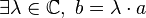
Et
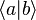
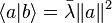
Finalement,
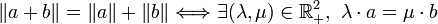
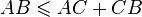
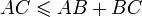
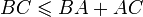
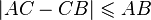
![AB = AC + CB \Leftrightarrow C \in [AB]](https://static.techno-science.net/illustration/Definitions/autres/b/b0998e2695cd70b9795e6baf16695461_2ef42d3eb8afeb1104bb2daf02dc3e67.png)