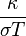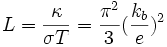Modèle de Drude - Définition

Conductivité thermique d'un métal

Il convient de doubler l'équation de transport du courant (c’est-à-dire de transport des particules) par une équation de transport de la chaleur :

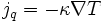
on obtient alors que le rapport des conductivités thermique et électrique est directement proportionnel à la température, le coefficient de proportionnalité étant désigné par le nombre de Lorenz :

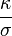
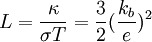
Cette loi de proportionnalité est connue sous le nom de loi de Wiedemann et Franz. Le résultat numérique indiqué ci-dessus vaut à peu près la moitié des valeurs obtenues expérimentalement. L'utilisation de la théorie du transport et du modèle quantique permet d'accéder à une valeur plus proche de la réalité pour le rapport (c'est-à-dire le nombre de Lorenz), la valeur obtenue étant alors :