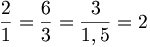Proportionnalité - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Algèbre |
| Logique |
| Arithmétique |
| Probabilités |
| Statistiques |
On dit que deux mesures sont proportionnelles quand on peut passer de l'une à l'autre en multipliant ou en divisant par une même constante non nulle. Dans le cas où l'on multiplie, cette constante est appelée coefficient de proportionnalité.
Exemple : si, dans un magasin, le prix des pommes est de 2 euros le kg, il y a proportionnalité entre la somme S à payer et le poids P de pommes achetées, ce que l'on note parfois:
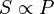
Le coefficient de proportionnalité est 2.
- Pour 1 kg, on doit payer 2 euros.
- Pour 3 kg, on doit payer 6 euros.
- Pour 1,5 kg, on doit payer 3 euros.
On remarque que le quotient des deux quantités est constant et est égal au coefficient de proportionnalité.
Les Anciens comme Euclide auraient écrit que 2 est à 1 comme 6 est à 3 ou comme 3 est à 1,5.
Tableau de proportionnalité
C'est un tableau où l'une des lignes est proportionnelle à l'autre.
| poids | 1 | 3 | 1,5 |
| prix | 2 | 6 | 3 |
On peut ajouter une colonne à un tableau de proportionnalité en additionnant deux colonnes, ou en multipliant une colonne par une constante.
- 3 + 1,5 = 4,5 et 6 + 3 = 9 donc
| poids | 1 | 3 | 1,5 | 4,5 |
| prix | 2 | 6 | 3 | 9 |
- 3 × 2 = 6 et 6 × 2 = 12 donc
| poids | 1 | 3 | 1,5 | 6 |
| prix | 2 | 6 | 3 | 12 |
Si on choisit deux colonnes, le produit des nombres situés dans une diagonale est égal au produit des nombres situés dans l'autre diagonale (produit en croix)
| 3 | 1,5 |
| 6 | 3 |
3 × 3 = 6 × 1,5
Proportionnalité et géométrie
La proportionnalité en géométrie est principalement utilisée dans le théorème de Thalès et dans les triangles semblables. Mais on la retrouve aussi dans les coordonnées de vecteurs colinéaires. En dimension 2, l'égalité des produits en croix ab' = ba' devient alors ab' - ba'= 0 (déterminant nul)
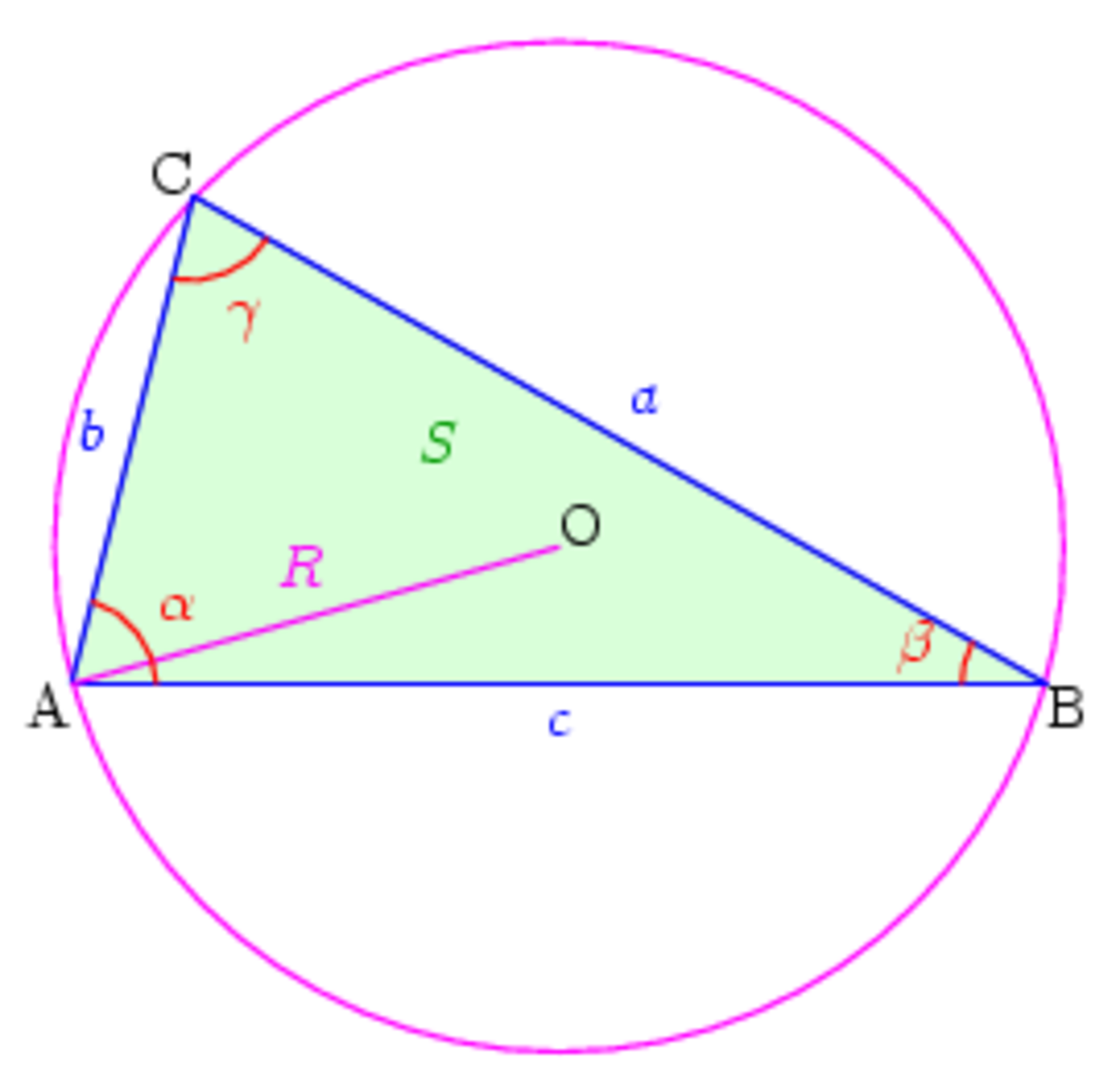
En géométrie plane, la loi des sinus affirme une relation de proportionnalité entre les longueurs et les sinus des angles d'un triangle. Sa démonstration repose sur la règle du produit en croix. Soit ABC un triangle du plan euclidien. Les longueurs des segments [BC], [CA] et [AB] sont notés a, b et c respectivement. On note α, β et γ les mesures des angles en A, B et C. Les notations sont indiquées sur la figure ci-contre. La longueur h de la hauteur issue de A peut se calculer de deux manières. Si H est le projeté orthogonal de A sur la droite (BC), les relations métriques dans les triangles rectangles ABH et ACH donnent :
- AH = csin(β) = bsin(γ).
Le calcul des longueurs des autres hauteurs donne de mene :
- asin(β) = bsin(α) et asin(γ) = csin(α).
La règle du produit en croix implique que (a,b,c) est proportionnel a (sinα,sinβ,sinγ) (loi des sinus). Cette loi est énoncée sous la forme
-
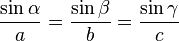
Dans le traité de géométrie d'Euclide, deux triangles ABC et A'B'C' du plan euclidien sont définis comme semblables s'ils ont mêmes mesures d'angles. La loi des sinus implique alors que les longueurs AB, BC, et CA sont proportionnelles à A'B', B'C' et C'A'. La condition "être semblables" équivaut à l'existence d'une similitude du plan euclidien envoyant ABC sur A'B'C'. La similitude multiplie toutes les longueurs par un même coefficient k appelé le rapport de la similitude. Il vaut le coefficient de proportionnalité entre les longueurs (AB, BC, CA) et (A'B', B'C', C'A').
En géométrie vectorielle, deux vecteurs v et w d'un même espace vectoriel E sont dits colinéaires s'il existe un scalaire a tel que v=aw. Posons leurs coordonnées dans une base de E
-
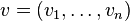
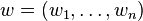
Alors les vecteurs v et w sont colinéaires ssi (v1,...,vn) est proportionnel à (w1,...,wn).