Modes de Floquet - Définition

Introduction

Les modes de Floquet, du nom du mathématicien français Achille Marie Gaston Floquet, sont une application du théorème de Floquet. C'est un outil mathématique utilisé pour l'étude et le développement des structures rayonnantes périodiques, comme les Antenne réseau à commande de phase.

Application à une structure périodique unidimensionnelle

Grâce au théorème de Floquet, le champ dans une structure périodique avec des conditions aux limites peut être exprimé comme une somme infinie d'ondes planes.

Soit une structure périodique de période d selon l'axe z. Un mode de Floquet dans une telle structure satisfait la relation :

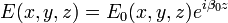
où β₀ est un paramètre qui dépend déterminé à partir des conditions aux limites de la structure. E₀(x,y,z) est une fonction périodique de z satisfaisant :

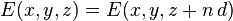
pour . Puisque E₀ est une fonction périodique, elle peut être représentée sous la forme d'une série de Fourier :

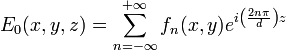
Substituant cette expression dans la précédente, on obtient :

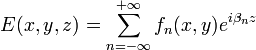
avec . f_n représente les coefficients de Fourier, définis par la formule :

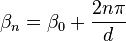
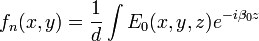
Le champ a ainsi été exprimé en fonction d'un nombre infini de composantes d'ondes propagatives, appelées harmoniques d'espace. Les nombres d'onde de la n-ième harmonique est β_n et est généralement complexe, même lorsque les pertes sont nulles. Il est important de souligner que chacune de ces harmoniques d'espace est une composante de Fourier du champ total et ne peut pas exister indépendamment.