Pic de Hubbert - Définition

Introduction

Le géophysicien Marion King Hubbert suggéra dans les années 1940 que la courbe de production d'une matière première donnée, et en particulier du pétrole, suivait une courbe en cloche (voir ci-contre). Cette courbe devint célèbre quand il en fit une présentation officielle à l'American Petroleum Institute en 1956, avec deux points importants :

• cette courbe en cloche passe par un maximum, indiquant que la production décline forcément par la suite,
• elle est relativement symétrique par rapport à ce maximum.

L'extrapolation de la première partie de la courbe devait permettre de la tracer en totalité, et par intégration, d'en déduire les réserves de pétrole d'une région donnée, ainsi que le maximum de production.

Hubbert en déduisit que la production de pétrole américaine (48 États) passerait par un maximum en 1970. Sa présentation fut peu appréciée par ses pairs, et oubliée jusqu'en 1971, année où la production américaine atteignit son maximum puis déclina, conformément à ses prédictions.

Ses travaux furent exhumés, et l'on tenta d'appliquer ses conclusions à des champs, des zones géographiques et même à la production mondiale. Mais en 1973 et 1979, survinrent les deux chocs pétroliers qui donnèrent à la courbe une forme radicalement différente de la courbe de Hubbert, pour laquelle on perdit à nouveau de l'intérêt.

Beaucoup plus tard, avec la disponibilité des moyens de calcul informatique, certains auteurs attribuèrent à la courbe de Hubbert une formule mathématique, plus pratique pour calculer l'intégrale de la courbe et faire des prévisions, voir calculs ci-dessous. Cette formule, ajoutée à la grande disponibilité de chiffres décrivant les productions pétrolières du monde, donna à de nombreux auteurs la possibilité de faire des investigations et des prédictions sur la production mondiale de pétrole. La courbe ci-contre montre la modélisation de la production P(t), courbe en cloche, et du volume extrait cumulé Q(t), courbe en S.

Modélisation de la production

La courbe de production a été modélisée par la formule suivante :

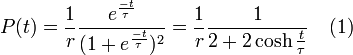
Cette formule ci-dessus est une simplification d'une formule plus générale :

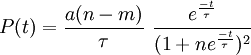
qui dérive elle-même de :

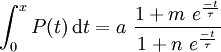
Cette équation est fréquemment appelée "logistic curve" en anglais, termes qui évoquent autre chose pour les francophones.

En effet, si maintenant on utilise les conventions suivantes :

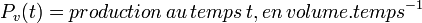
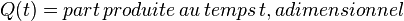
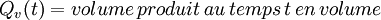
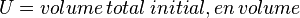
Il vient :

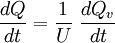
L'équation (1) vérifie l'équation de Verhulst :

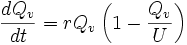
qui elle, est bien appelée "équation logistique" en français.

Ce type d'équation a été considérablement utilisé en dehors du domaine du pétrole, particulièrement dans le cadre de la modélisation de la croissance des populations (Équations de Lotka-Volterra) ; sous une autre forme, elle s'inclut dans la théorie du chaos, sous le nom de "logistic map" en anglais.

Si maintenant on fait l'approximation suivante : alors la production annuelle c'est-à-dire qu'elle est définie par une parabole d'intersection zéro et U. C'est cet ensemble de calculs qui a été mis à profit pour déterminer graphiquement U, soit la quantité de réserves pétrolières initiales.

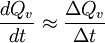
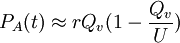
Il ne semble pas qu'on trouve, dans les travaux des différents auteurs, une justification de l'utilisation de cette courbe ; les supporteurs de cette méthode soulignent simplement qu'elle s'applique très bien aux États-Unis ; certains auteurs ont fait des tests systématiques sur de nombreux pays et trouvent des résultats variables ; enfin la méthode appliquée à l'ensemble de la planète fournit des résultats très approximatifs. La forme de la courbe, ainsi que ses implications, font qu'on l'appelle également "Pic de Hubbert".