Problème de l'obstacle - Définition
La liste des auteurs de cet article est disponible ici.
Recherche intuitive de la solution
Etablissons un raisonnement afin de trouver une solution explicite au problème de l'obstacle où χ(t) = 1 − 2t2 et g = 0. L'obstacle est donc une parabole symétrique.
Forme de la solution près des bords
Proposition — Sur  est une droite.
est une droite.
Démonstration — D'après un corollaire du lemme de Dubois-Raymond, u' est égale à une constante a presque partout. Or,
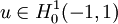
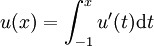
Et puisque u' est égale à une constante a presque partout, alors u(x) = a(x + 1).
La proposition suivante montre que la solution ne peut « couper » l'obstacle, sans quoi l'inégalité sur u'' n'est pas vérifiée.
Proposition — Soit
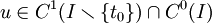
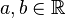
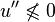
Démonstration — En utilisant les propriétes des dérivées des distributions et en prenant a et b très proches de t0 il est possible de construire une fonction test
![\varphi\in \mathcal{D} (]a,b[), \ \varphi \geq 0](https://static.techno-science.net/illustration/Definitions/autres/1/1723b5323e0afd06f8f5934b32d83c93_9afdccbe0fdb734571c884d25e683683.png)
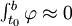
 .
.Extensions du problème
Obstacle non concave
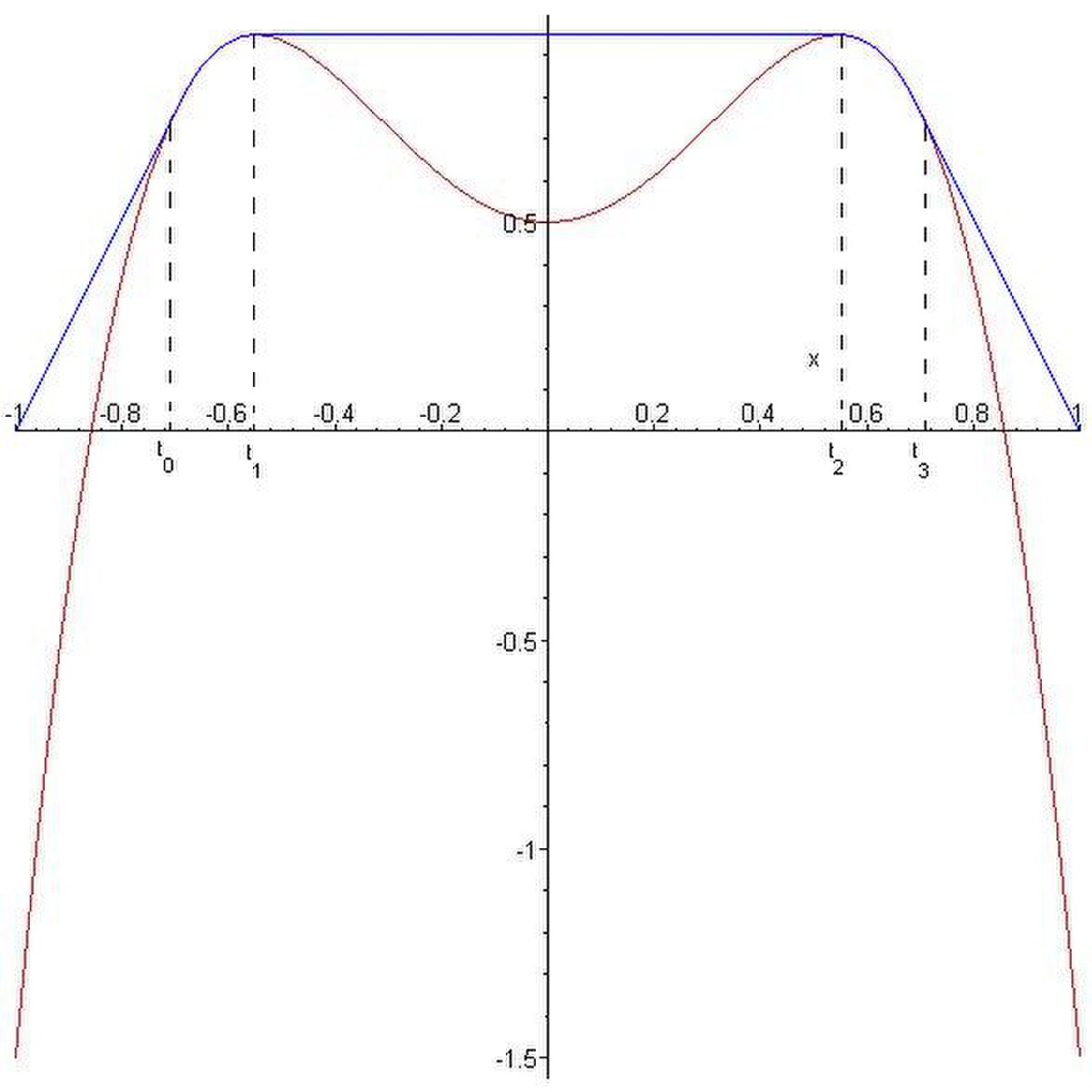
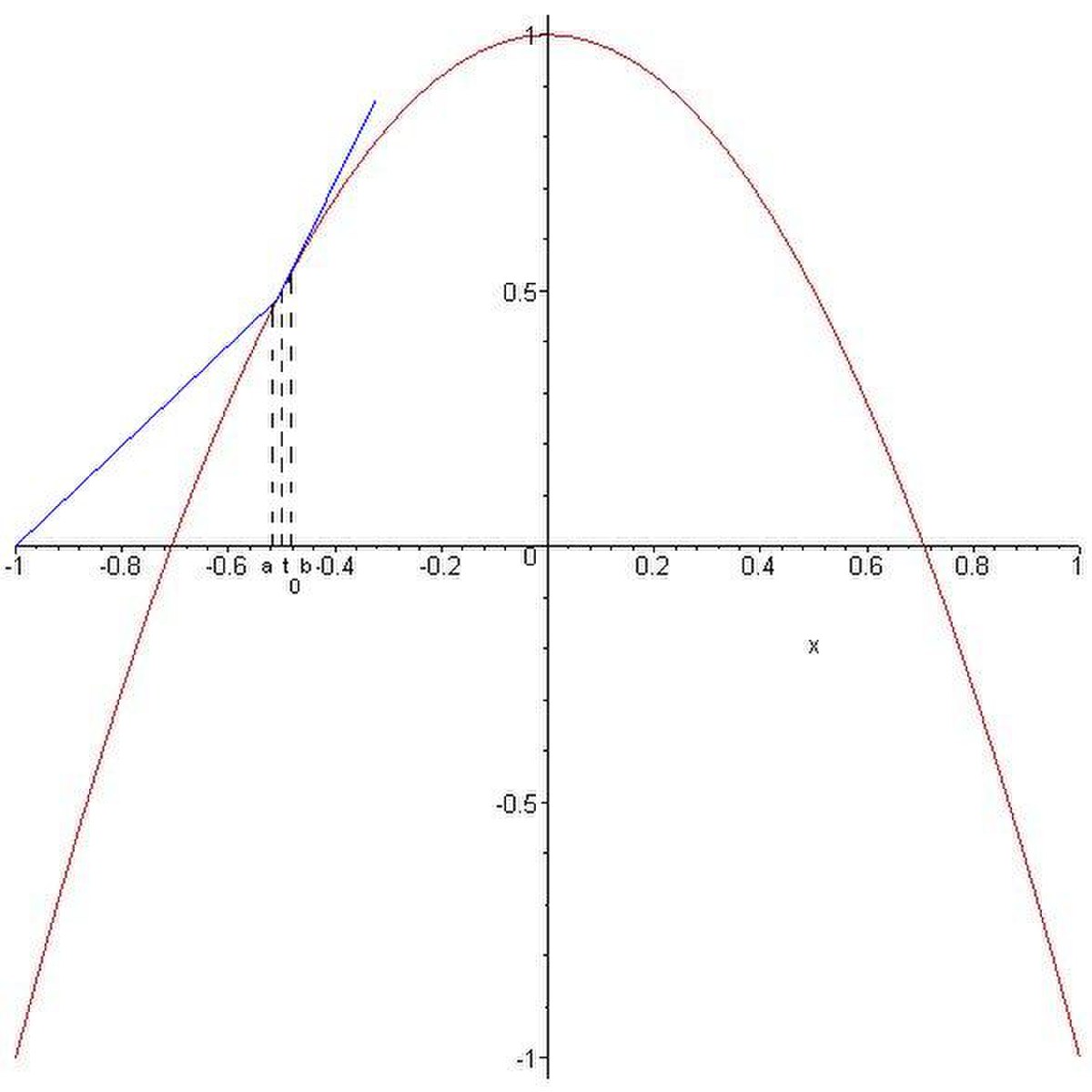
Considérons maintenant un autre obstacle, à savoir : χ(t) = − 5t4 + 3t2 + 0,5 sur I = [ − 1,1]. Le raisonnemement établi lors de l'étude de l'obstacle précédent nous laisse penser que la solution éventuelle serait de la forme (voir Fig. 4):
![u(t) = \left\{ \begin{array}{ll} a(t + 1) & t\in [-1,t_0]\\ \chi (t) & t\in [t_0,t_1]\\ \chi (t_1)= \chi (t_2) & t\in [t_1,t_2]\\ \chi (t) & t\in [t_2,t_3]\\ -a(t - 1) & t\in [t_3,1] \end{array} \right.](https://static.techno-science.net/illustration/Definitions/autres/f/feb5069102624d70024668dfbed0c019_9c84dd9194c0267ec5925289eded1ecc.png)
où
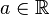
- a(t + 1) est la tangente de χ au point d'abscisse t0 s'annulant en − 1 ,
- χ(t) atteint son maximum sur [ − 1,0] au point t1;
- Par symétrie, comme χ est une fonction paire, t1 = − t2 et t3 = − t0. Ainsi, χ(t) atteint son maximum sur [0,1] au point t2 et − a(t − 1) est la tangente de χ au point d'abscisse t3 s'annulant en 1.
Cette solution vérifie bien le théorème de Stampacchia car
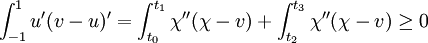
et est donc l'unique solution.
Double obstacle
En considérant maintenant le convexe fermé
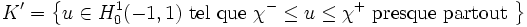
on peut alors étudier le problème à deux obstacles. Considérons les obstacles χ − (t) = − 5t4 + 3t2 + 0,5 et χ + (t) = 4t2 + 0,7 sur I = [ − 1,1].
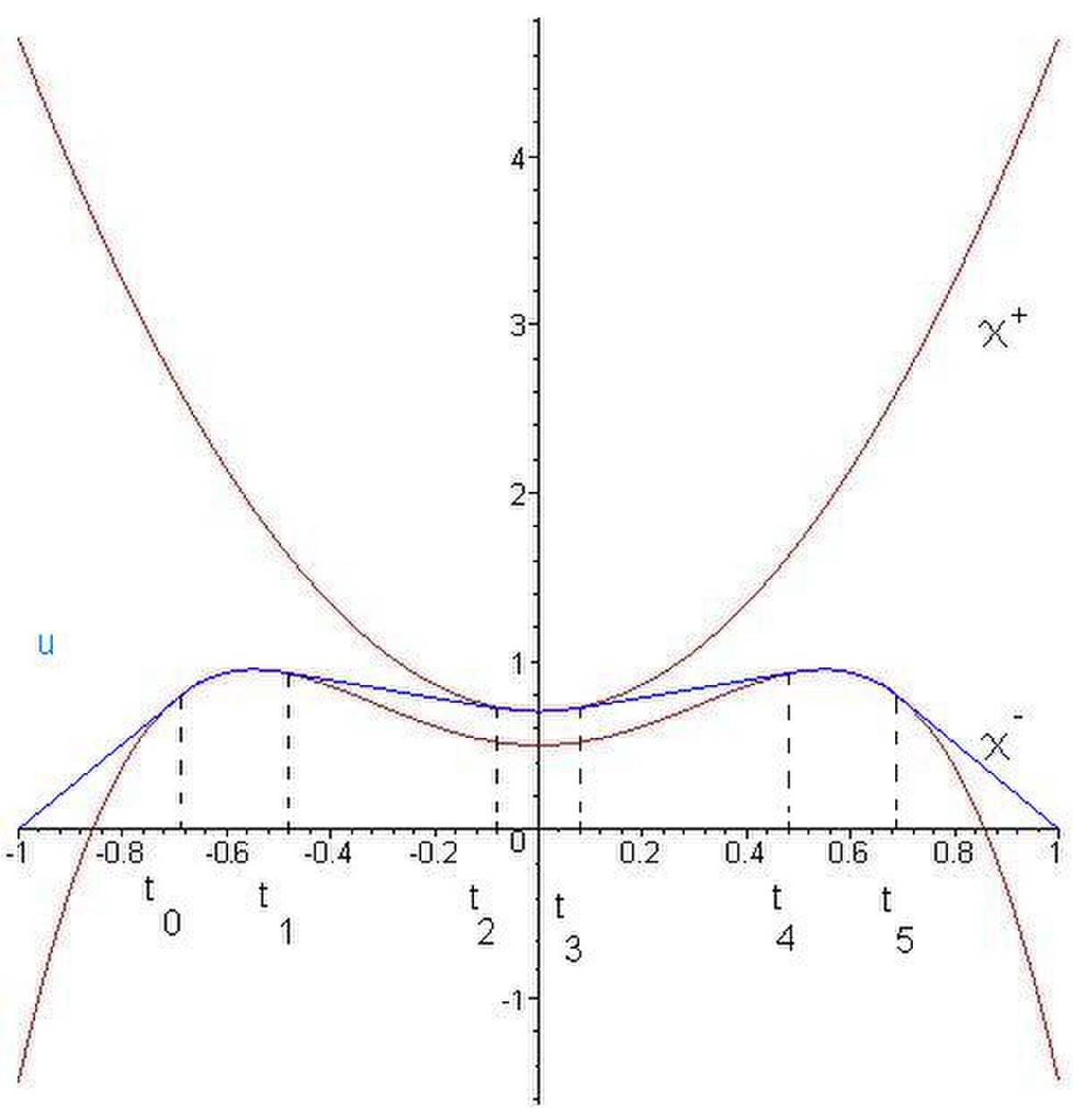
Le raisonnemement établi précédemment laisse penser que la solution éventuelle serait de la forme (voir Fig. 5):
![u(t) = \begin{cases} at + a\, & t\in [-1,t_0]\\ \chi^- (t) \ & t\in [t_0,t_1]\\ bt+c\, & t\in [t_1,t_2]\\ \chi^+ (t) \ & t\in [t_2,t_3]\\ -bt+c\, & t\in [t_3,t_4]\\ \chi^- (t) \ & t\in [t_4,t_5]\\ -at + a\, & t\in [t_5,1] \end{cases}](https://static.techno-science.net/illustration/Definitions/autres/1/1310d3f3a2840bcab1a4d1a688c7ed1e_cc0ef00896f01554c6a9be0510411f6a.png)
où
- at + a est la tangente de χ − au point d'abscisse t0 s'annulant en − 1,
- bt + c est la tangente commune aux deux obstacles. Elle est la tangente de χ − au point d'abscisse t1 et est la tangente de χ + au point d'abscisse t2.
- Par symétrie, comme χ − et χ + sont deux fonctions paires, t0 = − t5, t1 = − t4 et t2 = − t3. Ainsi, − bt + c est la tangente de χ + au point d'abscisse t3 et est la tangente de χ − au point d'abscisse t4 et
− at + a est la tangente de χ − au point d'abscisse t5 s'annulant en 1.
Par les mêmes calculs que précédemment, il est facile de voir que cette solution vérifie le théorème de Stampacchia et est donc l'unique solution.
Problème en dimensions ≥ 2
Enfin, ce problème peut être étudié en dimension supérieure utilisant alors la notion de gradient à la place des dérivées. Une des applications physiques est le recouvrement d'un objet par une membrane élastique.