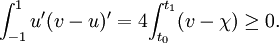Problème de l'obstacle - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le problème de l'obstacle est un problème classique de mécanique. Pour visualiser ce problème, il faut imaginer une membrane recouvrant un objet appelé alors obstacle (tel un film cellophane recouvrant un rôti de boeuf !). En effet, ce problème consiste à trouver une courbe solution u qui a une position très précise par rapport à l'obstacle et qui en plus vérifie une propriété de minimisation de longueur.
Pour mieux appréhender le problème, considérons-le en dimension 1. La membrane est alors un élastique recouvrant un objet. Cet élastique qui se trouve toujours au-dessus de l'objet tend à minimiser sa longueur. De plus, pour de petites variations, minimiser sa longueur revient à minimiser son énergie, en effet paramétrant l'élastique sur l'intervalle [ − 1,1] par
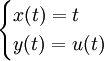
pour
![t \in [-1,1]](https://static.techno-science.net/illustration/Definitions/autres/b/b0f00d24484b160274d161593dc45cf4_f00dcd2157a097690d462e0983b426a3.png)
la longueur de l'élastique entre − 1 et 1 est :
Nous voudrions minimiser cette longueur, c'est-à-dire trouver
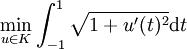
Or, si u' est suffisamment petit, nous avons
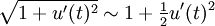
Minimiser la longueur de l'élastique revient donc à trouver
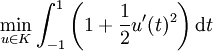
ce qui revient à minimiser
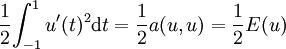
Approche théorique
Existence et unicité
Le problème de l'obstacle peut être vu comme une application du théorème de Stampacchia, en considérant la proposition suivante:
Proposition — L'espace de Hilbert
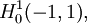
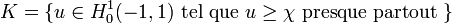
où
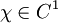
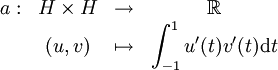
et la forme linéaire continue
vérifient les hypothèses du théorème de Stampacchia.
(Les démonstrations se font aisément en utilisant les inégalités de Hölder et de Poincaré.)
Le théorème de Stampacchia s'applique donc, et ainsi il existe un unique
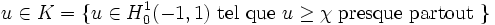
tel que :
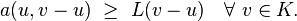
Ce qui est équivalent à dire qu'il existe un unique

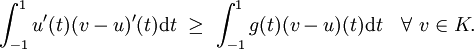
De plus, a étant symétrique, alors u est caractérisé par la propriété :
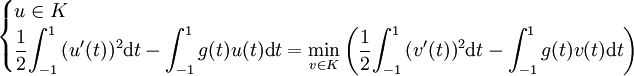
Propriétés de la solution
Démontrons à présent quelques propriétés vérifées par la solution u, en utilisant la dérivée seconde de u. Cependant
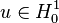
Proposition — Avec les notations du théorème de Stampacchia,
-
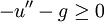
- − u'' − g = 0 au sens des distributions sur
 .
.
- Pour la première assertion : soit
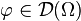
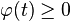
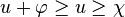
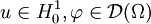
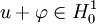
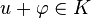
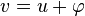
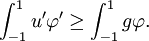
Ainsi, en passant aux distributions :
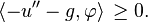
Donc
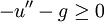
- Pour la seconde assertion : ω est un ouvert. Soit
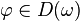
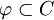
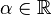
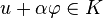
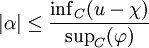
nous obtenons
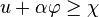
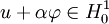
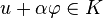
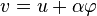
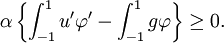
Comme α prend des valeurs positives ou négatives, alors
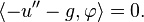
Comparaison d'énergies
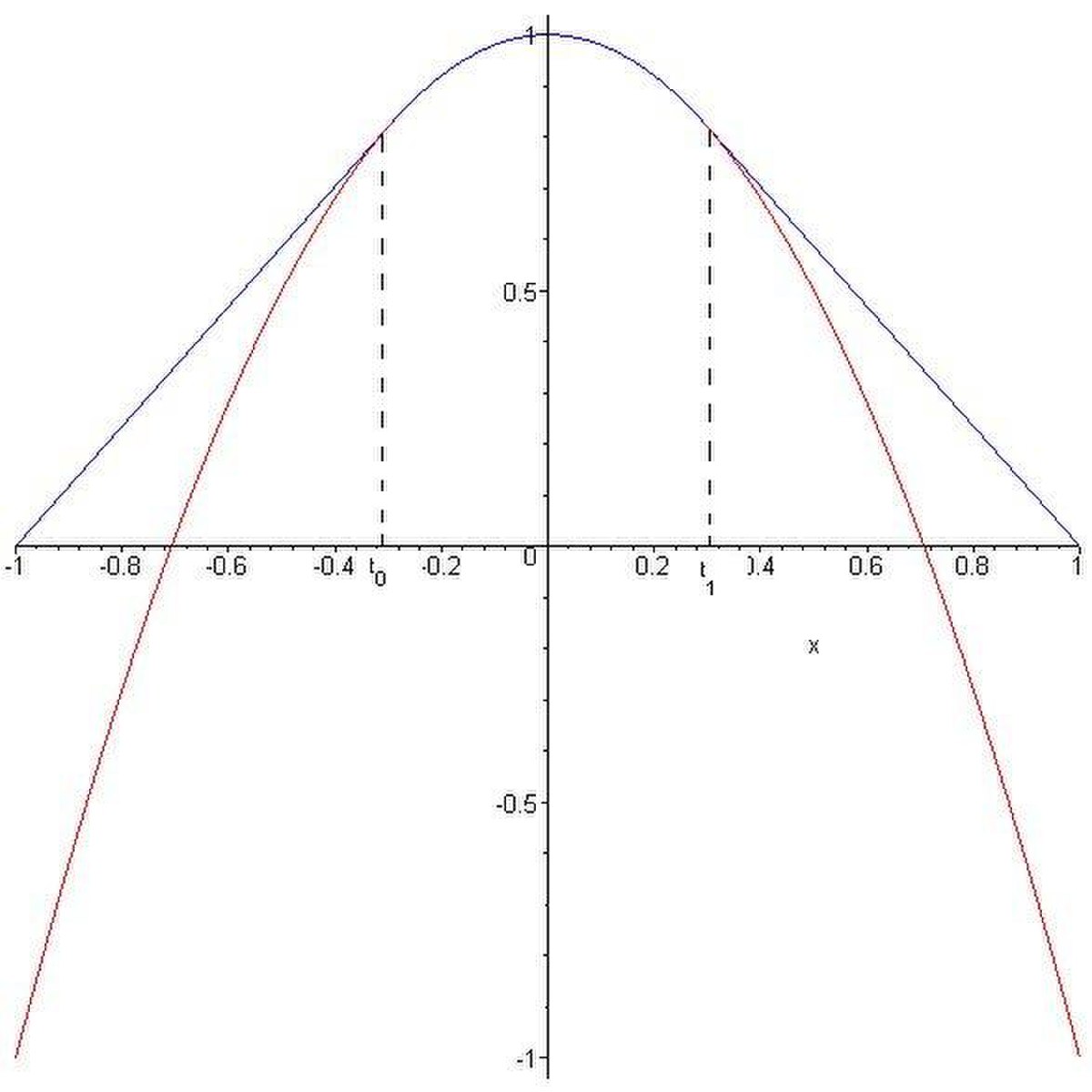
Proposition — Soit T0 la tangente à χ au point d'abscisse
![t_0\in [-1,0]](https://static.techno-science.net/illustration/Definitions/autres/0/02d2f2e0e0cad39e90d4855ee22abc94_88ff43db9b7aac79d0ad1ebf113fd179.png)
![t_1\in [0,1]](https://static.techno-science.net/illustration/Definitions/autres/a/a9542ab16f3fb839fe144cef22a47747_744e93035b93b7875f91fa9a098343dd.png)
![u(t) = \left\{ \begin{array}{ll} T_0(t) \ & t\in [-1,t_0],\\ \chi (t) \ & t\in [t_0,t_1],\\ T_1(t) \ & t\in [t_1,1]. \end{array} \right.](https://static.techno-science.net/illustration/Definitions/autres/a/af4972da1485cd7d63939ec6f5751435_60b5417f89ff67c5a15c742563756892.png)
![u_1(t) = \left\{ \begin{array}{ll} T_0(t) \ & t\in [-1,0],\\ T_1(t) \ & t\in [0,1]. \end{array} \right.](https://static.techno-science.net/illustration/Definitions/autres/8/894c6ac17c3b80280a1fea239a15a55e_17d85c09152591be6106ff6bcd31fc86.png)
- L'énergie de u,
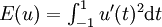
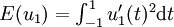
- En considérant u1 telle qu'elle a été définie précédemment et u2 un triangle centré (voir figure 2), l'énergie de u2 est supérieure à celle de u1.
- L'énergie d'un triangle décentré u3 est supérieure à celle d'un triangle centré u2 (voir figure 2).
- Soit
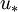
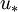
Démonstration — Les démonstrations se font facilement en calculant la dérivée pour chaque fonction. Quant à la solution tordue, il faut considérer
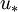
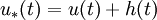
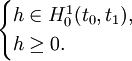
Conclusion
La solution semble donc être (voir Fig. 3)
![u(t) = \begin{cases} T_0(t) \ & t\in [-1,t_0],\\ \chi (t) \ & t\in [t_0,t_1],\\ T_1(t) \ & t\in [t_1,1]. \end{cases}](https://static.techno-science.net/illustration/Definitions/autres/c/c102186401d1b842766cd5c1025da751_06915d71013e2399380e31af6ea398e4.png)
et on vérifie facilement que c'est le cas car cette solution vérifie le théorème de Stampacchia qui garantit son unicité :