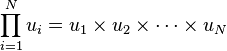Produit (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Généralisation
Plus généralement, un produit est le résultat de la composition de deux éléments d'un ensemble pour une loi interne multiplicative. Lorsque des matrices ou des objets de diverses autres algèbres associatives sont multipliés, le produit dépend en général de l'ordre des facteurs ; en d'autres termes, la multiplication des matrices, et les lois de multiplication de ces autres algèbres, ne sont pas commutatives.
Des généralisations et des extensions du concept de produit existent en mathématiques :
- le produit scalaire et le produit vectoriel sont des sortes de multiplications de vecteurs ;
- le produit matriciel, la multiplication des matrices n'est pas commutative sauf sur des sous-ensembles triviaux;
- le produit usuel de deux fonctions ;
- les produits dans des anneaux ou dans des corps de toutes sortes.
Des multiplications respectant l'invariance des normes (« la norme du produit de deux objets est égale au produit de leur norme ») n'ont pu être définies que pour quelques objets : les réels, les complexes, les quaternions et les octonions.
Produit indexé
Le produit peut être noté ∏ (pi capitale) lorsque de nombreux facteurs indexés interviennent. Par exemple, si l'on considère une suite