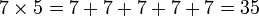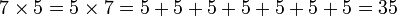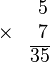Produit (mathématiques) - Définition

Introduction

On nomme produit de nombres entiers, réels, complexes ou autres le résultat d'une multiplication, ou expression qui identifie les facteurs à multiplier.

L'ordre dans lequel les nombres réels ou les nombres complexes sont multipliés, de même que la façon de regrouper ces termes, n'ont pas d'importance; ainsi nulle permutation de termes ne modifie le résultat du produit. Ces propriétés sont nommées commutativité de la loi et associativité de la loi de multiplication.

Les multiplications d'objets comme les vecteurs et les matrices (produit matriciel, produit tensoriel, etc.) ne sont en revanche pas commutatifs.

Cas simples et notations

Le principe de base de la multiplication est de compter le nombre d'éléments contenu au total par un ensemble de paquets (multiplicateur) contenant chacun le même nombre d'élément (multiplicande).

Vocabulaire

Le premier membre de l'opération est nommé par convention multiplicande et le second multiplicateur; cette distinction n'a pas de conséquence fonctionnelle, à la différence de celle de dividende et de diviseur.

multiplicande × multiplicateur

L'opérateur est noté par le signe multiplication « × », un point « . » sur la ligne quand le séparateur décimal est la virgule et un point opérateur « ⋅ » (médian) lorsque le point sur la ligne sert déjà de séparateur décimal, comme dans la convention anglo-saxonne ; en programmation informatique, les langages utilisent en général l'astérisque « * » (signe étoile). Il est omis quand il est présent sans ambigüité, par exemple dans une expression comme 3a.

Principe pour les nombres entiers

Dans le cas des nombres entiers, la multiplication revient à faire des additions de nombres identiques, par exemple :

La multiplication étant commutative, l'ordre des facteurs n'influe pas sur le résultat :

Ces expressions se lisent respectivement « 7 fois 5 » et « 5 fois 7 ».

Cette opération peut aussi se noter, pour les besoins de la technique,

Le résultat peut être obtenu :

• par consultation d'un répertoire de résultats connus, tel qu'une table de multiplication
• par l'exécution d'un algorithme (de tête, à la main avec un instrument d'écriture, ou à l'aide d'un calculateur).
  • l'algorithme le plus simpliste se résume en additions successives (fréquent pour les petits nombres, mais rapidement inutilisable)
  • pour des nombres plus grands mais encore de taille raisonnable, il existe des méthodes plus efficaces qui font partie du bagage culturel
  • l'informatique moderne a suscité des techniques encore plus élaborées, certaines étant des objets de recherche

Principe pour les nombres décimaux

Un nombre décimal est un nombre entier qui a été divisé par une puissance de dix (1 — c'est alors un entier —, 10, 100, 1 000…). La distributivité de la multiplication sur la division permet de calculer les multiplications de nombres décimaux comme celle des nombres entiers :

1. on ignore les virgules et l'on multiplie les nombres comme si c'étaient des entiers ;
2. le nombre de chiffres après la virgule du résultat final est la somme du nombre de chiffre après la virgule du multiplicande et du multiplicateur.

Par exemple :

pour calculer

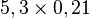
• on calcule , ce qui donne 1 113 ;
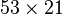
• le multiplicande a un chiffre après la virgule, le multiplicateur en a deux, le résultat en a donc trois (1+2) : le résultat final est 1,113.