Programme de Langlands - Définition

Prix

Les parties du programme concernant les corps locaux ont été complétées en 1998 par Michael Harris, Richard Taylor et Guy Henniart et concernant les corps de fonctions en 1999. Laurent Lafforgue a reçu la médaille Fields en 2002 pour son travail sur le cas du corps de fonctions. Ce travail prolongeait les recherches menées par Vladimir Drinfeld, pour lesquelles celui-ci a reçu la médaille Fields en 1990. Seuls des cas particuliers concernant les corps de nombres ont été démontrés, certains par Langlands lui-même.

Langlands a reçu le Prix Wolf en 1996 et le prix Nemmers de mathématiques en 2006 pour son travail sur ces conjectures. Laurent Lafforgue (en 2000), Gérard Laumon et Bảo-Châu Ngô (en 2004), Michael Harris et Richard Taylor (en 2007) et Jean-Loup Waldspurger (en 2009) ont reçu le Clay Research Award pour leurs travaux sur le programme.

Idées conduisant au programme de Langlands

Dans un contexte très large, le programme a été construit sur des idées existantes : la philosophie des formes cusp formulée quelques années plus tôt par Israel Gelfand, le travail et l'approche d'Harish-Chandra sur les groupes de Lie semi-simples, et en termes techniques la formule des traces de Selberg et d'autres.

Ce qui, initialement, était très novateur dans le travail de Langlands, excepté la profondeur technique, était de proposer une connexion directe à la théorie des nombres, mêlée avec la structure organisationnelle hypothétique (ce qui a été appelé fonctorialité).

Par exemple, dans le travail d'Harish-Chandra, on trouve le principe de ce qui peut être fait pour un groupe de Lie semi-simple (ou réductif), ce qui pourrait être fait pour tous. Par conséquent, une fois que le rôle de certains groupes de Lie de dimension basse tels que dans la théorie des formes modulaires a été reconnu, et rétrospectivement, avec dans la théorie des corps de classes, la voie est ouverte aux spéculations pour au moins pour n > 2.

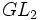
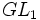
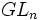
L'idée de forme cuspidale provient des courbes cuspidales dans les courbes modulaires mais aussi a un sens visible dans la théorie spectrale comme un « spectre discret », qui contrastait avec le « spectre continu » des séries d'Eisenstein. Elle devint beaucoup plus technique pour les groupes de Lie plus grands, parce que les sous-groupes paraboliques sont plus nombreux.

Et, du côté des formes modulaires, il y avait des exemples tels que les formes modulaires de Hilbert, les formes modulaires de Siegel, et les fonctions thêta.

Bibliographie

• Pierre Colmez, Elements d'analyse et d'algèbre (et de théorie des nombres), Editions de l'Ecole Polytechnique
• Stephen Gelbart, An Elementary Introduction to the Langlands Program, Bulletin of the AMS v.10 no. 2, avril 1984
• Edward Frenkel, Lectures on the Langlands Program and Conformal Field Theory, hep-th/0512172
• J. Bernstein, S. Gelbart, An Introduction to the Langlands Program