Programme de Langlands - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Relation avec la théorie des nombres - Un principe général de fonctorialité - Le contexte des représentations automorphes - Prix - Idées conduisant au programme de Langlands - Bibliographie

Introduction

En mathématiques, le programme de Langlands est, en 2010, un domaine de recherche actif et fertile en conjectures. Ce programme souhaite relier la théorie des nombres aux représentations de certains groupes. Il a été proposé par Robert Langlands en 1967.

Relation avec la théorie des nombres

La première étape du programme, réalisée bien avant les travaux de Langlands, peut être vue comme la théorie des corps de classes. La loi de réciprocité d'Artin (en) s'applique à une extension de corps de nombres algébriques dont le groupe de Galois est abélien, et considère les représentations de dimension 1 de ce groupe de Galois à valeurs dans le groupe multiplicatif du corps de base. Plus précisément, des fonctions L associées à ces représentations unidimensionnelles sont identiques à certaines séries L de Dirichlet (les analogues de la Fonction zêta de Riemann construites à partir des caractères de Dirichlet). La correspondance entre ces différentes sortes de fonctions L constitue la loi de réciprocité d'Artin.

Pour les groupes de Galois non-abéliens et pour leurs représentations de dimensions plus élevées, on peut encore définir les fonctions L d'une manière naturelle : les fonctions L d'Artin.

Un principe général de fonctorialité

Langlands généralisa encore son programme : à la place du groupe linéaire général $GL_n\,$ , d'autres groupes réductifs peuvent être considérés. De plus, en se donnant un tel groupe G, Langlands construit un groupe de Lie ${}^L\!G\,$ , puis, pour chaque représentation cuspidale automorphe de G et chaque représentation de dimension finie de ${}^L\!G\,$ , il définit une fonction L. Une de ses conjectures prédit que ces fonctions L satisfont une certaine équation fonctionnelle généralisant celles des fonctions L les mieux connues.

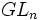
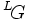
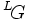
Puis, il formule un « principe de fonctorialité » très général. Deux groupes réductifs et un morphisme entre les groupes L correspondants étant donnés, cette conjecture relie leurs représentations automorphes d'une manière qui est compatible avec leurs fonctions L. Cette conjecture de fonctorialité implique toutes les conjectures présentées jusque là. Cette construction est d'une nature analogue à celle des représentations induites - qui, dans la théorie plus traditionnelle des formes automorphes a été appelée un relèvement, est connue dans certains cas particuliers, et est covariante (tandis qu'une représentation restreinte est contravariante). Les tentatives pour obtenir une construction directe n'ont produit que des résultats conditionnels.

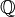
Toutes ces conjectures peuvent être formulées pour des corps plus généraux à la place de $\mathbb{Q}\,$ : les corps de nombres algébriques (le cas originel et le plus important), les corps locaux, et les corps de fonctions (extensions finies de $F_{p}(t)\,$ où p est un nombre premier et $F_{p}(t)\,$ est le corps des fonctions rationnelles sur le corps fini à p éléments).

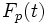
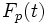
Le contexte des représentations automorphes

La premier pas de Langlands fut de trouver la généralisation appropriée des fonctions L de Dirichlet qui permettraient la formulation de l'énoncé d'Artin dans un cadre plus général.

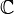
Auparavant, Hecke a relié les fonctions L de Dirichlet avec les formes automorphes (fonctions holomorphes sur le demi-plan supérieur de $\mathbb{C}\,$ qui satisfont certaines équations fonctionnelles). 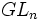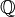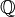Langlands généralisa alors celles-ci aux représentations cuspidales automorphes, qui sont certaines représentations irréductibles de dimension infinie du groupe général linéaire $GL_{n}\,$ sur l'anneau adélique de $\mathbb{Q}\,$ . (Cet anneau garde une trace de tous les complétés de $\mathbb{Q}\,$ , voir nombres p-adiques).

Langlands associa des fonctions L à ces représentations automorphes, et conjectura que chaque fonction L d'Artin issue d'une représentation de dimension finie d'un groupe de Galois d'un corps de nombres est égale à une fonction L issue d'une représentation cuspidale automorphe. Ceci constitue la « conjecture de réciprocité de Langlands ».