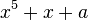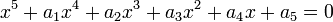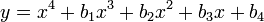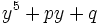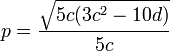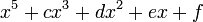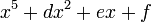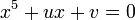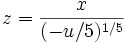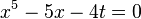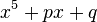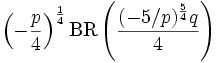Radical de Bring - Définition

Introduction

En mathématiques et en algèbre, un radical de Bring ou ultraradical est un zéro réel du polynôme

dans lequel a est un nombre complexe.

George Jerrard (1804-1863) a montré que certaines équations quintiques peuvent être résolue par radicaux et par radicaux de Bring, qui ont été introduits par Erland Samuel Bring (1736-1798).

La forme normale de Bring-Jerrard

Si

puis si

nous pouvons obtenir un polynôme de degré 5 en y, une transformation de Tschirnhaus, par exemple en utilisant le résultant pour éliminer x. Nous pouvons alors chercher les valeurs particulières des coefficients qui forment les coefficients du polynôme en y de la forme

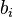
Cette réduction, découverte par Bring et redécouverte par Jerrard, est appelée une forme normale de Bring-Jerrard. Une attaque directe pour une réduction en forme normale de Bring-Jerrard ne fonctionnera pas ; l'astuce est de le faire par paliers, en utilisant plusieurs transformations de Tschirnhaus, ce qui est réalisé relativement facilement avec un système informatique algébrique.

D'abord, en substituant à la place de x, on enlève le terme de trace (degré quatre). Nous pouvons alors employer une idée due à Tschirnhaus pour éliminer aussi le terme en , en fixant et en résolvant en p et q pour éliminer les termes en et en , nous trouvons que et

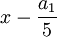
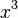
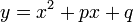
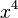
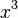
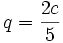
élimine les deux termes du troisième et quatrième degré de

Nous pouvons maintenant écrire

dans

et éliminer aussi le terme en degré deux, d'une manière qui ne nécessite pas de solution d'équation supérieure au degré trois. Ceci demande de prendre les racines carrées pour les valeurs de , et , et de trouver la racine d'une équation cubique pour .

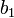
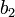
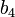
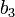
La forme générale est assez facile à calculer en utilisant un programme de calcul formel tel que Maple ou Mathematica, mais elle est assez désordonnée, il semble envisageable d'exploiter simplement la méthode, qui peut être appliquée dans n'importe quel cas particulier. On peut établir un système de trois équations, puis les résoudre pour les coefficients . Une des solutions ainsi obtenue sera décrite, impliquant les racines d'un polynôme de degré pas plus haut que trois ; en prenant le résultant avec les coefficients ainsi calculés réduit l'équation en forme normale de Bring-Jerrard. Les racines de l'équation originale sont maintenant exprimables en termes de racines de l'équation transformée.

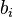
Regardée comme une fonction algébrique, les solutions de

impliquent deux variables, u et v, néanmoins la réduction est actuellement en une fonction algébrique d'une variable, très analogue à une solution par radicaux, puisque nous pouvons de plus réduire la forme de Bring-Jerrard. Par exemple, si nous formons

alors nous réduisons l'équation sous la forme

qui entraîne x comme une fonction algébrique de variable unique t.

Solution pour l'équation quintique générale

Nous pouvons maintenant exprimer les racines de n'importe quel polynôme

en termes de radical de Bring radical sous la forme

et ses quatre conjugués. Nous avons réduit en forme de Bring-Jerrard en termes d'équations polynômiales résolubles, et nous avons utilisé les transformations impliquant des expressions polynômiales en racines jusqu'au quatrième degré, ce qui signifie que l'inversion de la transformation peut être faite en trouvant les racines d'un polynôme résoluble par radicaux. Cette méthode produit des solutions superflues, mais lorsque nous avons trouvé les solutions correctes numériquement, nous pouvons aussi écrire les racines de la quintique en termes de racines carrées, racines cubiques, et le radical de Bring, qui est par conséquent une solution algébrique en termes de fonctions algébriques d'une seule variable - une solution algébrique d'une quintique générale.