Résultant - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, le résultant est une notion qui s'applique à deux polynômes. Elle est utilisée en théorie de Galois et en théorie algébrique des nombres. Le résultant de deux polynômes est un scalaire qui permet de vérifier s'ils possèdent des facteurs communs. Il peut être calculé à partir des coefficients des polynômes à l'aide d'un déterminant. On peut aussi l'obtenir à partir des racines des polynômes si ceux-ci sont scindés.
Définition et expression
Définition
Soient A un anneau commutatif unitaire intègre, P et Q deux polynômes de degré respectifs n et m à coefficients dans A. Les coefficients des polynômes sont notés ai et bi, on a donc les égalités :
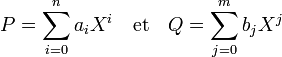
-
- Le résultant des deux polynômes P et Q est le déterminant de leur matrice de Sylvester. Il est noté dans cet article R(P, Q).
Expression
Avec les notations ci-dessus, le résultant est le déterminant de la matrice M suivante :
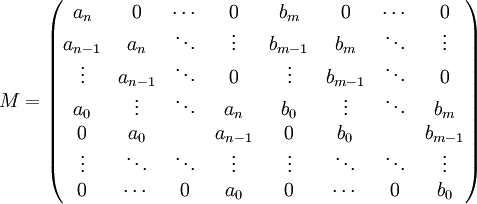
La représentation choisie ici diffère de l'article détaillé. Elle évite une transposition pour exprimer les propriétés du résultant. Comme la transposition ne modifie pas le déterminant, les deux conventions peuvent être choisies.
Applications
Si x et y sont deux nombres algébriques tels que P(x) = Q(y) = 0, on vérifie aisément que z = x + y est racine du résultant des deux polynômes (en x) P(x) et Q(z − x), ce qui prouve que x + y est aussi algébrique ; en considérant de même xpQ(z / x), on montrerait également que xy est algébrique, et en définitive que les nombres algébriques forment un corps. Une application un peu plus élaborée de la même idée permet d'ailleurs de montrer que ce corps est algébriquement clos.
Une application naturelle du résultant est le discriminant. Cette notion correspond au résultant d'un polynôme et de sa dérivée. Par delà l'intérêt de la résolution d'une équation polynômiale de degré deux, le discriminant permet de déterminer si un polynôme admet des racines multiples ou non. Cette propriété est importante en théorie de Galois car la théorie est différente si une extension n'est pas séparable. En théorie algébrique des nombres le discriminant est une propriété associé à un anneau de Dedekind. Même si la définition est différente, il peut encore se calculer à l'aide d'un résultant. Cette notion est alors intimement liée à celle de norme arithmétique.
Le résultant est un outil permettant de déterminer l'intersection de deux courbes algébriques (c'est le théorème de Bézout) ou la multiplicité d'un point sur une hypersurface.
En théorie de l'information le résultant est utilisé pour des calculs d'arithmétique modulaire permettant de calculer des diviseurs communs à deux polynômes, en général sur un corps fini.
Propriétés
Expressions à l'aide du déterminant
La matrice de Sylvester est de taille n + m, avec les n premières lignes linéaires en le polynôme P, les m suivantes en le polynôme Q :
-
- Le résultant vérifie les formules :
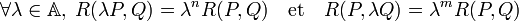
La modification de l'ordre des colonnes modifie le signe du déterminant en fonction de sa signature :
-
- Le résultant vérifie la formule :
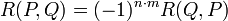
L'endomorphisme φ de l'espace des polynômes de degré inférieur ou égal à n + m - 1 et de matrice M peut être vu comme une application de l'identité de Bézout. Si A (resp. B) est un polynôme de degré n - 1 (resp. m - 1) :
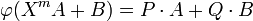
Si P et Q ne sont pas premiers entre eux, ils ont un facteur commun C et P (resp. Q) est égal à un produit du type C.P1 (resp. C.Q1). L'égalité suivante :
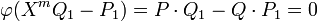
montre qu'alors φ n'est pas injectif et le résultant est nul. Réciproquement une considération de degré montre que si P et Q sont premiers entre eux l'endomorphisme est injectif donc de déterminant non nul :
-
- Le résultant est non nul si et seulement si les deux polynômes P et Q sont premiers entre eux.
Expressions à l'aide des racines
La lettre F désigne le corps des fractions de A et K une extension de F contenant toutes les racines des deux polynômes, notées αi pour P et βj pour Q.
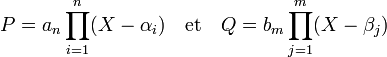
Quitte à travailler dans K et non plus dans A, les deux polynômes sont scindés, c'est-à-dire qu'ils se décomposent en produit de polynômes du premier degré et ils admettent chacun autant de racines que leur degré. L'usage de l'extension K offre une nouvelle expression du résultant.
-
- Le résultant des polynômes P et Q s'exprime de la manière suivante :
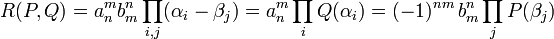
Cette formule montre par exemple que translater les deux polynômes ne change pas leur résultant :
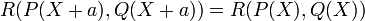
Si on ajoute à P un multiple de Q, seul le coefficient du second membre est susceptible d'être modifié.
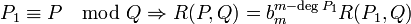
En suivant un algorithme analogue à celui d'Euclide on obtient un procédé de calcul de résultant en temps quadratique.
Supposons dans un premier temps que les deux polynômes soient unitaires, c'est-à-dire que an et bm soient égaux à un. Chaque coefficient de P et de Q s'exprime comme le produit d'un polynôme symétrique en les racines. Si le pième polynôme symétrique d'ordre q est noté σpq :
![\forall i \in [0, n-1],\; a_i = (-1)^i\sigma_{in}(\alpha_1,\cdots,\alpha_n)\quad\text{et}\quad \forall j \in [0, m-1],\; b_j = (-1)^j \sigma_{jm}(\beta_1,\cdots,\beta_m)](https://static.techno-science.net/illustration/Definitions/autres/7/78a689853690920bdd624d77585caa59_4c98313ee5b8355dcaab55b6e70701a7.png)
Le résultant peut être vu comme un polynôme en les différentes racines de P et Q, il existe un polynôme Rr en n + m variables, tel que :
![R(P,Q)= R_r[\alpha_1,\cdots,\alpha_n,\beta_1,\cdots,\beta_m]\;](https://static.techno-science.net/illustration/Definitions/autres/b/b0726f35e12cc28e4372ec6412bbd56b_2f55e4922fe2e26f93839fa2ecb597a4.png)
L'anneau des polynômes à coefficients dans K et à m + n indéterminées est factoriel, Le polynôme Rr possède comme facteur (βj - αi) il existe un polynôme λ[X1, ..., Xn+m] tel que :
![R(P,Q) = \lambda[\alpha_1,\cdots,\alpha_n,\beta_1,\cdots,\beta_m]\prod_{i,j}(\beta_j - \alpha_i)\;](https://static.techno-science.net/illustration/Definitions/autres/6/68f2a5999e959c21a83f230a41c8eec5_e27922c72d98b67f126b236fd59197a4.png)
Une considération de degré montre que le polynôme λ[X1, ..., Xn+m] est constant. Il suffit de choisir judicieusement les polynômes P et Q, par exemple Xn et Xm pour s'assurer que la constante λ est égale à un. Pour traiter le cas où les polynômes ne sont pas unitaires, la première proposition du paragraphe précédent permet de conclure.

















































