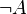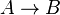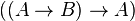Style de Fitch pour la déduction naturelle - Définition
La liste des auteurs de cet article est disponible ici.
Exemples
Nous donnons ci-dessous quelques exemples d'utilisation de la déduction naturelle. Dans la première partie, nous n'utiliserons pas la règle d'élimination de la double négation. Dans la deuxième partie, nous utiliserons cette règle. Les formules déduites dans cette deuxième partie ne sont pas reconnues valides par les mathématiciens intuitionnistes. Nous utiliserons les symboles suivants :

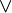
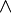


Exemples n'utilisant pas l'élimination de la double négation
Exemple 1 :
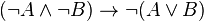
-
-
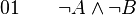
-

-

-

-

-

-

-

-

-

-

-
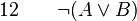
-
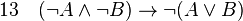
-
On montre que la réciproque
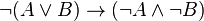
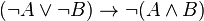
Exemple 2 :
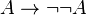
-
-

-

-

-

-
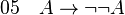
-
La réciproque
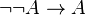
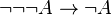
Exemple 3 :
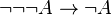
-
-
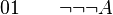
-

-
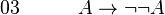
-

-

-

-
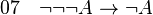
-
Exemples utilisant l'élimination de la double négation
Les exemples qui suivent utilisent l'élimination de la double négation. On peut montrer que cette utilisation est nécessaire. Ils ne sont donc pas acceptés en logique intuitionniste.
Exemple 4 :
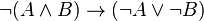
-
-
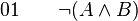
-
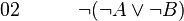
-
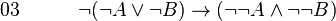
-
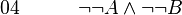
-

-

-
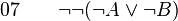
-
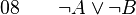
-
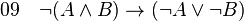
-
Exemple 5 : si
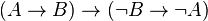
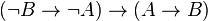
Exemple 6: On peut démontrer que
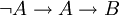
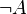

Exemple 7 : de même la démonstration de la validité du tiers exclu
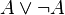
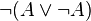
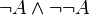
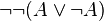
Si les intuitionnistes rejettent le tiers exclu, ils acceptent bien sûr le principe de non contradiction :
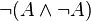
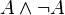
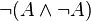
Exemple 7 connu sous le nom de loi de Peirce :
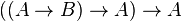
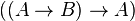
.ou bien on a A,
.ou bien on a