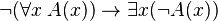Style de Fitch pour la déduction naturelle - Définition

Les règles relatives à la disjonction

Les deux règles de déduction pour la disjonction sont les suivantes.

La règle d'introduction de la disjonction ou règle de l'affaiblissement d'une thèse énonce que, à partir de la phrase P on peut déduire la phrase (P ou Q) aussi bien que la phrase (Q ou P), quelle que soit la phrase Q. Cette règle peut sembler peu intéressante mais elle est en vérité très importante. Parfois il est avantageux de déduire (P ou Q) après avoir prouvé P, car on peut savoir par ailleurs que (P ou Q) a d'autres conséquences.

(introduction de la disjonction à partir de 1)

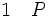
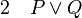
et de même

(introduction de la disjonction à partir de 1)

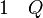
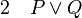
La règle d'élimination de la disjonction ou règle de la disjonction des hypothèses ou règle de la distinction des cas, stipule que, si on a prouvé (P ou Q) et qu'on a également prouvé (si P alors R) ainsi que (si Q alors R), alors on a prouvé R. Cette règle sert quand on examine plusieurs cas possibles qui conduisent à la même conclusion.

(hypothèse provisoire)

(propriété déduite de 2)

(introduction de l'implication entre 2 et 3)

(hypothèse provisoire)

(propriété déduite de 5)

(introduction de l'implication entre 5 et 6)

(élimination de la disjonction entre 1, 4, 7)

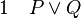
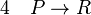
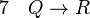
Les règles de déduction pour les quantificateurs

L’usage des noms de variable dans les théories du premier ordre

Les règles de déduction pour les opérateurs universels et existentiels gouvernent l’usage des noms de variable. Cet usage donne à une théorie la puissance de la généralité, c’est-à-dire la possibilité de connaître non chaque invividu pris isolément mais tous les individus d’un même genre, en une seule phrase.

Les règles d’usage des variables précisent à quelles conditions on peut introduire des noms de variable et ce qu’on peut alors dire à leur sujet. Ces règles sont naturelles mais il y a quelques difficultés techniques à propos des notions de terme, d’occurrence libre ou liée d’une variable, de substitution d’un terme aux occurrences d’une variable et de substitution d’une variable aux occurrences d’un terme.

Pour qu’une théorie puisse utiliser la logique du premier ordre il faut avoir défini un domaine d’objets et il faut que les prédicats attribués par la théorie à ses objets ne soient pas eux-mêmes des objets de la théorie.

La signification d’un nom de variable d’objet, c’est de représenter un objet quelconque de la théorie : soit x un nombre. Souvent on introduit un nom de variable dans des prémisses qui déterminent des conditions générales sur cet objet. x est un objet quelconque de la théorie pourvu seulement qu’il satisfasse à ces conditions : soit x un nombre premier ... Une théorie contient en général des noms pour ses objets. La théorie des nombres entiers contient par exemple des noms pour tous les nombres : 0, 1, 2, ..., -1, -2, ...

Les termes peuvent être simples ou composés. Ce sont les noms d’objet, les noms de variable d’objet, et toutes les expressions composées que l’on peut former à partir d’eux en appliquant les opérateurs d’objets de la théorie. Par exemple, 1, x, x+1et (x+x)+1 sont des termes de la théorie des nombres.

Rappelons d’abord la très importante distinction entre les variables liées par un opérateur et les autres, les variables libres. Les occurrences d’un nom de variable dans une phrase sont tous les endroits où ce nom apparait. Une occurrence peut être libre ou liée. Quand un opérateur existentiel ou universel en x est appliqué à une phrase complexe, toutes les occurrences de x deviennent liées par cet opérateur. Toutes les occurrences qui ne sont pas ainsi liées sont libres.

Si une phrase contient plusieurs opérateurs existentiels et universels, il est souhaitable que ces opérateurs portent tous sur des noms de variable différents. Cette règle n’est pas indispensable. Elle n’est pas respectée lorsque l’on met le calcul des prédicats sous la forme d’une algèbre cylindrique (une algèbre cylindrique est une algèbre de Boole complétée par des lois particulières aux opérateurs universels et existentiels). Mais elle est toujours respectée en pratique parce qu’elle permet d’éviter des confusions.

Une phrase est obtenue à partir d’une autre par substitution d’un terme t aux occurrences d’une variable x lorsque toutes les occurrences libres de x ont été remplacées par t. Par exemple, (le père de x est humain et le père de x est honnête) est obtenu par substitution du terme le père de x à la variable y dans la formule (y est humain et y est honnête).

Ces préliminaires permettent de formuler les règles de déduction pour les opérateurs universels et existentiels.

Les règles relatives au quantificateur universel

La règle d'introduction du quantificateur universel ou règle de généralisation énonce que, de P(x) on peut déduire (pour tout x, P(x)) pourvu que le nom de variable x n’apparaisse jamais dans les hypothèses dont P(x) dépend.

(introduction de quel que soit, où x n'est pas libre dans les prémisses de P)

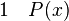
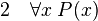
Très souvent on introduit des variables dans des hypothèses provisoires. On raisonne ensuite sur elles comme si elles étaient des objets. On peut alors en déduire des lois générales, parce que ce qu’on a déduit est vrai pour tous les objets qui vérifient les mêmes hypothèses. Ce sont les règles d’abandon d’une hypothèse provisoire et de généralisation qui permettent de conclure.

La règle d'élimination du quantificateur universel ou règle de singularisation énonce que, à partir d’une phrase de la forme (pour tout x) P(x), on peut déduire P(t), pour n’importe quel terme t dont les variables ne sont pas liées dans P(x). P(x) désigne une phrase quelconque qui contient x comme variable libre, P(t) désigne la phrase obtenue à partir de P(x) en y substituant t à toutes les occurrences libres de x. La règle de singularisation consiste simplement à appliquer une loi universelle à un cas singulier.

(élimination de quel que soit)

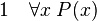
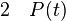
Les règles relatives au quantificateur existentiel

La règle d’introduction du quantificateur existentiel, ou règle des preuves directes de l’existence, énonce que, à partir de la phrase P(t), on peut déduire il existe un x tel que P(x) pour toute variable x qui n’apparait pas dans P(t) et pour tout terme t dont les noms de variables ne sont pas liés dans P(x).

P(t) désigne une phrase quelconque qui contient au moins une fois le terme t. P(x) est obtenue à partir de P(t) en substituant x à t à une ou plusieurs de ses occurrences. Dans cette règle il n’est pas nécessaire de substituer x à toutes les occurrences de t.

(introduction de il existe)

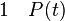
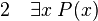
La règle d'élimination du quantificateur existentiel ou règle des conséquences de l’existence permet, à partir d'une proposition (il existe x, P(x)), d'introduire une nouvelle hypothèse provisoire P(y) où y est un nom de variable qui n’a jamais été utilisé auparavant et où P(y) est obtenu à partir de P(x) en substituant y à toutes les occurrences de x. On peut alors raisonner sous cette hypothèse. La règle des conséquences de l’existence permet alors de conclure de la façon suivante : de la phrase (il existe un x tel que P(x)) on peut déduire R lorsque R a été déduit sous l’unique hypothèse provisoire supplémentaire P(y) et que y n’apparait ni dans les prémisses antérieures à P(y) ni dans R. y est une sorte d’être hypothétique. Il ne fait que servir d’intermédiaire dans une déduction mais il n’apparait ni dans ses prémisses, ni dans sa conclusion.

(hypothèse)

(y variable nouvelle)

(déduction à partir de 2, ne faisant pas intervenir y)

(élimination de il existe dans 1 et 3)

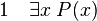
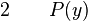
Exemples

Exemple 1

(hypothèse provisoire)

(hypothèse provisoire)

(y variable nouvelle à partir de 1)

(élimination de quel que soit dans 2)

(élimination de la négation 3, 4)

(élimination de il existe entre 1 et 5)

(introduction de la négation entre 2 et 6)

(introduction de l'implication 1, 7)

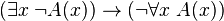
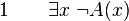
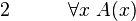
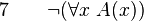
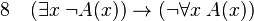
Exemple 2 : on a également , mais la preuve nécessite une élimination de la double négation, et ce théorème de la logique classique n'est pas accepté en logique intuitionniste.