Style de Fitch pour la déduction naturelle - Définition

Les règles relatives à la négation

La règle d'introduction de la négation énonce que, si on démontre une contradiction à partir d’une hypothèse P alors celle-ci est nécessairement fausse et donc sa négation est vraie. Ainsi, si dans une déduction sous l’hypothèse provisoire P, on a trouvé une contradiction (Q et non Q), notée également , alors on peut déduire nonP à partir de toutes les prémisses antérieures sauf P. Avec la méthode de Fitch, on décale donc (non P) sur la gauche par rapport à P, ce qui se représente comme suit :

(introduction de la négation entre 1 et 2)

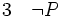
La règle d'élimination de la négation ou règle de la suppression de la double-négation ou raisonnement par absurde énonce que, de (non nonP) on peut déduire P. Il s'agit bien du raisonnement par l'absurde car dans, un tel raisonnement, pour prouver P, on suppose (non P) et l'on cherche à obtenir une contradiction. Si tel est le cas, on a prouvé (non non P) d'après la règle d'introduction de la négation, et c'est bien la règle de suppression de la double-négation qui permet de conclure à P :

(élimination de la double négation 1)

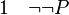
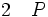
ou bien

(hypothèse provisoire [raisonnement par l'absurde])

(introduction de la négation entre 1 et 2)

(élimination de la double négation 3)

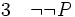
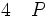
Quand on considère que toute phrase est nécessairement ou bien vraie ou bien fausse, la validité de cette dernière règle est évidente. Elle est caractéristique de la logique classique, qui est présentée ici et est utilisée par la grande majorité des scientifiques. Elle est parfois contestée à cause d’un problème important, celui des preuves d’existence par l’absurde. Il arrive que l’on puisse prouver qu’un problème a une solution sans être capable de la trouver. Pour cela il suffit de prouver que l’absence de solution conduit à une contradiction. Le raisonnement par l’absurde permet alors de conclure qu’il n’est pas vrai que le problème n’a pas de solution : non non (le problème a une solution). En logique classique, on supprime la double négation pour en conclure que le problème a une solution. Cependant, la démarche ainsi suivie ne fournit aucun procédé constructif de la solution cherchée. Cette objection fut soulevée par certains mathématiciens et logiciens, dont Brouwer, qui contestèrent cette méthode et s'opposèrent à Hilbert qui la défendait. Les mathématiciens constructivistes ou intuitionnistes estiment qu’une preuve d’existence n’a pas de sens si elle ne fournit pas également un procédé constructif de l'objet en question. Aussi ces derniers rejettent-ils la règle de suppression de la double négation pour lui substituer la règle suivante : de P et (non P), on peut déduire une contradiction, et de cette contradiction n'importe quelle proposition Q.

(élimination de la négation 2 en logique intuitionniste)

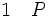
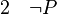
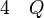
Dans les exemples, nous utiliserons cette deuxième règle d'élimination lorsqu'il est possible de se passer de la règle d'élimination de la double négation

On peut introduire d’autres règles pour les autres opérateurs booléens, notamment l’opérateur d’équivalence, mais ce n’est pas nécessaire, parce que ces opérateurs peuvent être définis à partir des précédents et que leurs règles de déduction peuvent être alors déduites à partir des règles précédentes. (P équivaut à Q) est défini par ( (si P alors Q) et (si Q alors P) ) .