Surfaces de Scherk - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Les deux surfaces de Scherk ont été découvertes en 1834. Il s'agissait des premières nouvelles surfaces minimales sans intersection découvertes depuis l'hélicoïde.
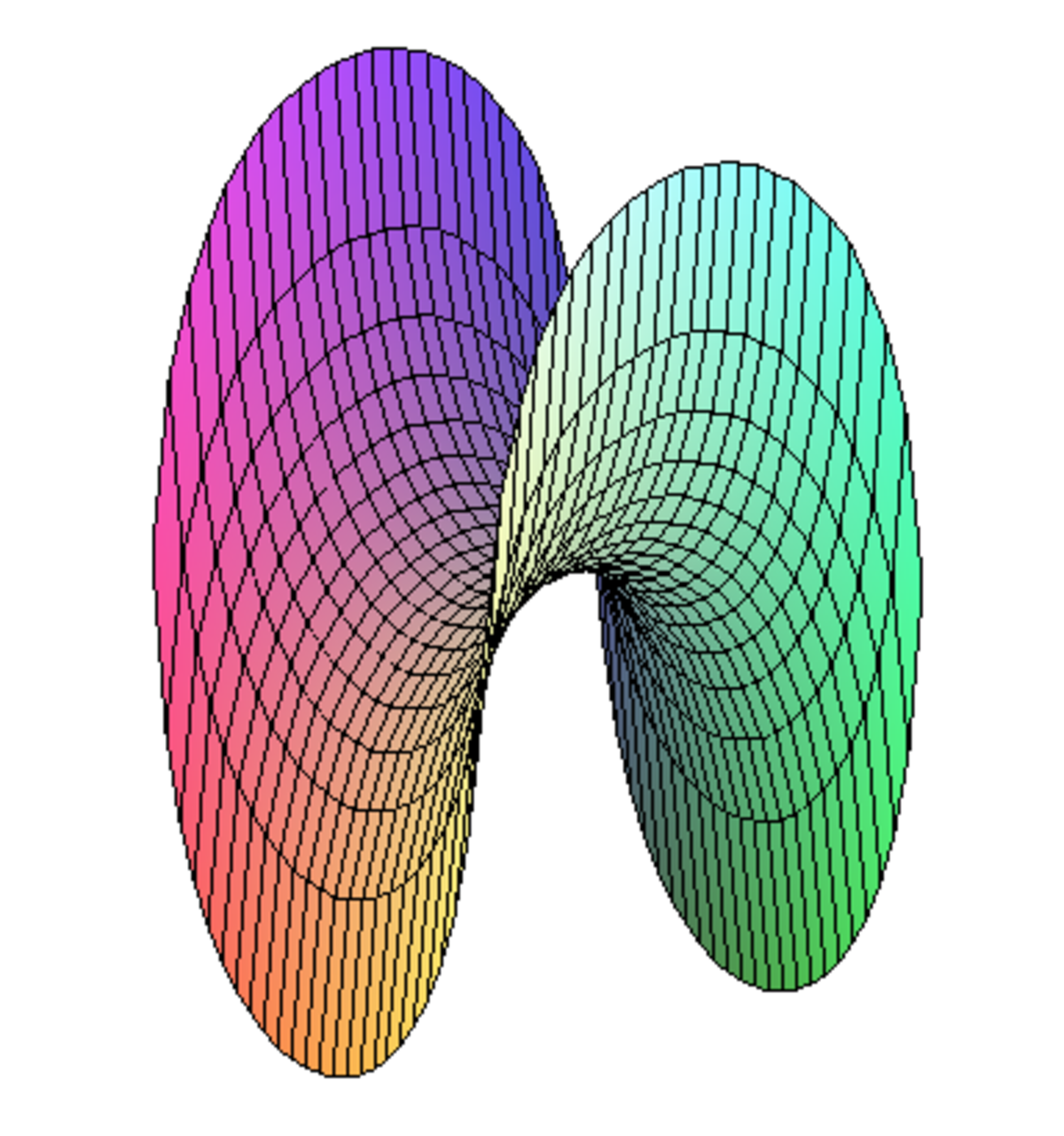
Une période de la première surface de Sherk.
La première surface de Scherk est doublement périodique, définie par l'équation implicite :
La seconde surface de Scherk peut être écrite sous forme paramétrique :
pour
![\theta \in \left[0,2\pi\right]](https://static.techno-science.net/illustration/Definitions/autres/c/c1178e51e2c9be2d08c407f292cf4f85_5ef7822d67f395489df0a46b60f9a6e0.png)
![r \in \left[0,1\right]](https://static.techno-science.net/illustration/Definitions/autres/5/5699d32df2558fc9b8975d51bb109623_4445d2d89878f477e26528f2da159a09.png)
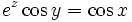
![x = 2 \Re \left[ \ln{\left(1+r e^{i\theta} \right)} - \ln{\left(1 - r e^{i\theta}\right)} \right]](https://static.techno-science.net/illustration/Definitions/autres/3/377f7017a22f2672a0853cc0a4cfad43_6ed2bbf9709aacba23817df67a582906.png)
![y = \Re \left[ \frac{4 i}{\tan{\left(r e^{i\theta}\right)}} \right]](https://static.techno-science.net/illustration/Definitions/autres/2/2c7822e7acaccc97b0cf722711f31908_5cbe6ba3a2458553ee5627899fa78110.png)
![z = \Re \left[ \ln{\left(1+r^2 e^{2i\theta}\right)} - 2i \ln{\left(1-r^2 e^{2i\theta}\right)}\right]](https://static.techno-science.net/illustration/Definitions/autres/7/774531a9dee9590cdb8bb7cd020efd32_f09ea058d95628c5054a5efbc0c64182.png)

















































