Théorème de Borel-Cantelli - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Théorème de Borel-Cantelli (théorie de la mesure) - Limite supérieure d'ensembles - Loi du zéro-un de Borel - Lemme de Borel-Cantelli (probabilités)

Introduction

Dans la théorie des probabilités, le lemme de Borel-Cantelli, parfois aussi appelé théorème de Borel-Cantelli, concerne une suite d'événements. Sous une forme un peu plus générale, il est également valable en théorie de la mesure. Le lemme stipule que :

Lemme de Borel-Cantelli — Si la somme des probabilités d'une suite $\scriptstyle\ (A_n)_{n\ge 0}$ d'événements d'un espace probabilisé $\scriptstyle\ \left(\Omega, \mathcal A, \mathbb{P}\right)\$ est finie, alors la probabilité qu'une infinité d'entre eux se réalisent simultanément est nulle.

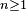
L'indépendance des événements n'est pas nécessaire. Par exemple, considérons une suite $\scriptstyle\ (X_n)_{n\ge 1}$ de variables aléatoires, telle que, pour tout $\scriptstyle\ n\ge 1$ ,

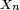
La somme des $\scriptstyle\ \mathbb{P}(X_n = 0)$ est finie, donc d'après le lemme de Borel-Cantelli la probabilité que $\scriptstyle\ X_n = 0$ se produise pour une infinité d'indices $\scriptstyle\ n$ est 0. En d'autres termes, avec une probabilité de 1, $\scriptstyle\ X_n$ est non nul à partir d'un certain rang (aléatoire) $\scriptstyle\ n_0.$ On a donc appliqué le lemme de Borel-Cantelli à la suite d'évènements $\scriptstyle\ (A_n)_{n\ge 0}$ définie par

Théorème de Borel-Cantelli (théorie de la mesure)

Pour un espace mesuré général $\scriptstyle\ (X,\mathcal{A},\mu)$ , le lemme de Borel-Cantelli prend la forme suivante :

Théorème de Borel-Cantelli — Soit $\scriptstyle\ (A_n)_{n\ge 0}$ une suite dans $\scriptstyle\ \mathcal{A}$ . Si

alors

Posons

et remarquons que

$\scriptstyle\ B_n\$ est une suite décroissante (pour l'inclusion) d'éléments de $\scriptstyle\ \mathcal{A},$ car $\scriptstyle\ B_n= A_n\cup B_{n+1}$ ;
pour tout $\scriptstyle\ n\ge 0,$ on a $\scriptstyle\ \mu(B_n)<+\infty.$

Le deuxième point découle de la majoration

et de l'hypothèse du théorème de Borel-Cantelli, selon laquelle $\scriptstyle\ \mu(A_n)\$ est le terme général d'une série convergente. Les 2 conditions permettant de conclure que

sont ainsi remplies. De plus $\scriptstyle\ \mu(B_n)\$ est majorée par

qui est le reste d'une série convergente, donc

Comme

on conclut que

CQFD

Limite supérieure d'ensembles

Définition — La limite supérieure $\scriptstyle \limsup_n\, A_n$ d'une suite $\scriptstyle\ (A_n)_{n\ge 0}\,$ de parties d'un ensemble $\scriptstyle \Omega$ est l'ensemble des éléments $\scriptstyle \omega$ de $\scriptstyle \Omega$ tels que l'assertion $\scriptstyle \{\omega\in A_k\}$ soit vérifiée pour une infinité d'indices $\scriptstyle k\ge 0$ .

En d'autres termes, on peut dire que $\scriptstyle\ \omega\in\limsup_n\, A_n$ si et seulement si l'ensemble $\scriptstyle \{k\ge 0\ \vert\ \omega\in A_k\}$ est infini, ou bien non borné. Une formulation équivalente est la suivante : pour tout $\scriptstyle n\ge 0$ , on peut trouver $\scriptstyle k\ge n$ tel que $\scriptstyle \omega\in A_k$ . Cette dernière formulation fournit une écriture commode de la limite supérieure d'ensembles à l'aide d'opérations élémentaires sur les ensembles :

Sous l'influence de la terminologie anglo-saxonne, on dira aussi parfois que $\scriptstyle\ \omega\in\limsup_n\, A_n$ si et seulement si $\scriptstyle\ \{\omega\in A_k\}\$ "infiniment souvent" ou bien "infinitely often", d'où la notation rencontrée dans certains ouvrages :

Finalement, remarquons que la définition " $\scriptstyle\ \omega\in\limsup_n\, A_n$ si et seulement si $\scriptstyle\ \omega\$ appartient à une infinité de $\scriptstyle\ A_k\$ " peut induire en erreur : si par exemple toutes les parties $\scriptstyle\ A_k\$ sont égales, il se peut que $\scriptstyle\ \omega\$ appartienne à $\scriptstyle\ A_k\$ pour une infinité d'indices $\scriptstyle\ k\$ , et il se peut donc que $\scriptstyle\ \omega\$ appartienne à $\scriptstyle\ \limsup_n\, A_n,$ sans pour autant qu' $\scriptstyle\ \omega\$ appartienne à une infinité de $\scriptstyle\ A_k\$ (puisqu'il n'existe, au fond, qu'un seul $\scriptstyle\ A_k$ ).

Loi du zéro-un de Borel

Le lemme de Borel-Cantelli ne doit pas être confondu avec la loi du zéro-un de Borel, parfois appelée second lemme de Borel-Cantelli :

Loi du zéro-un de Borel — Si les événements $\scriptstyle\ A_n$ sont indépendants, alors $\scriptstyle\ \mathbb{P}\left(\limsup_n A_n\right)$ vaut 0 ou 1 suivant que la série de terme général $\scriptstyle\ \mathbb{P}(A_n)$ est convergente ou divergente.

La loi du zéro-un de Borel montre en particulier que l'hypothèse $\scriptstyle\ \sum_{n\ge 0}\mu(A_n)<+\infty$ du lemme de Borel-Cantelli ne peut en aucun cas être affaiblie en $\scriptstyle\ \lim_{n}\mu(A_n)=0$ . En effet on peut avoir simultanément, d'une part $\scriptstyle\ \lim_{n}\mathbb{P}(A_n)=0$ , d'autre part (indépendance des $\scriptstyle\ A_n$ et $\scriptstyle\ \sum_{n\ge 0}\mathbb{P}(A_n)=+\infty$ ), donc on peut avoir simultanément :

Lemme de Borel-Cantelli (probabilités)

- Introduction - Théorème de Borel-Cantelli (théorie de la mesure) - Limite supérieure d'ensembles - Loi du zéro-un de Borel - Lemme de Borel-Cantelli (probabilités)

Cette forme de vie géante ne ressemble à rien d'autre de connu 🌎

Recherche: cette nouvelle molécule se montre terriblement efficace contre la calvitie 🔬

Des tardigrades génétiquement modifiés pour survivre... sur le Soleil ☀️

Or, cuivre... pourquoi ces métaux précieux se trouvent dans les zones de subduction ? 🌋

Une avancée majeure dans la supraconductivité à haute température 🌡️

Les chimpanzés fabriquent leurs outils comme des ingénieurs 🛠️

Mach 16: des surprises physiques découvertes dans les vols hypersoniques 🚀

Des scientifiques ont réussi à filmer la séparation des brins de l'ADN 🧬

Comment 13 degrés peuvent transformer une foule en chaos ? 🚶‍♂️

Découverte: les phoques savent évaluer la quantité d'oxygène dans leur sang 🤿

Les trous noirs pourraient-ils protéger la vie dans l'Univers ? 🌱

Implants mammaires en silicone: une toxicité remise en question

Découverte d'un "broyeur d'étoiles" dans notre galaxie 🌀

Neandertal et Sapiens: une collaboration inattendue il y a 100 000 ans 🤝

Que sont ces sphères noires découvertes sur Mars ? 🔴

Découverte: les champignons contre... la grippe 🍄

Découverte inédite: voici comment notre cerveau attache les souvenirs entre eux 🖇️

Découverte: les requins émettent des sons ! 🦈

Des scientifiques inventent un ciment qui aspire le CO2 🌎

Comment le cerveau décode le temps: du récit aux réseaux neuronaux 🕰️

Horloge atomique dans son smartphone et GPS 1000 fois plus précis ⏱️

L'ocytocine: l'hormone de l'amour ou simple mythe ? 💕

Cette nouvelle méthode permettrait d'identifier une vie extraterrestre inattendue 👽

Une araignée géante filmée dans les abysses de l'Antarctique 🕷️

Trois familles d'objets planétaires identifiées dans le Système Solaire externe 🔭

Découverte d'une griffe géante à 2 doigts appartenant à une nouvelle espèce de dinosaure 🦖

Un nouvelle technologie de vaisseaux nucléaires pour explorer le Système solaire 🚀

Votre cerveau se consomme lui-même pour rechercher de l'énergie, pendant un exercice intense 🏃

Des vestiges organiques découverts sur Mars 🧐

Pourquoi les armes nucléaires sont-elles si difficiles et dangereuses à produire ? 💥

MRAM: la mémoire informatique du futur enfin là ? ⚡

Vidange d'un lac glaciaire: la catastrophe du Sikkim en 2023 expliquée 🌊

Qu'est-ce qui a bien pu creuser ces tunnels il y a plusieurs millions d'années ? ⛏️

Les secrets biologiques de Maria Branyas Morera, la supercentenaire 🕰️

Exploiter la rotation terrestre pour produire de l'électricité: l'énergie verte de demain ? ⚡

Que nous apprennent ces émissions radioactives de météorites lunaires et martiennes ? ☢️

La Chine dévoile un processeur quantique fiable à 99.9% 🚀

Voici les emblématiques espèces éteintes que la science pourrait bientôt ressusciter 🦣

Un poisson de 15 millions d'années incroyablement préservé 🐟

Existence démontrée d'un lien entre muscles, cerveau et fertilité 💪

Prévision météo: une petite IA surclasse les plus gros supercalculateurs 🌤️

Cette fosse commune révèle une histoire de violence extrême et de respect ⚔️

Cette nouvelle cellule solaire dure 10 fois plus longtemps 🌞

Des poulets aux plumes de dinosaures: une expérience génétique étonnante 🐔

Vidéo: une pieuvre chevauche un requin, une rencontre marine insolite 🐙

Une explication aux magnétars à faible champ 🧲

Découverte d'une galaxie géante improbable 🌀

Connaissez-vous cette montagne, aux vents dépassant 300 km/h ? 🏔️

L'énergie noire se serait "inversée", l'hypothèse qui explique certaines observations 🤔

COVID-19, cancer... vers une production en masse d'anticorps artificiels ⚔️

Page générée en 0.116 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise