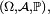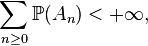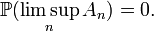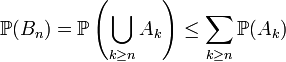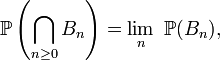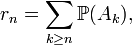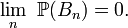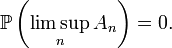Théorème de Borel-Cantelli - Définition
La liste des auteurs de cet article est disponible ici.
Lemme de Borel-Cantelli (probabilités)
Un espace probabilisé
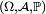
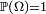

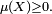
La démonstration est en tout point identique à celle du théorème précédent. On pose
et on remarque que

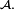

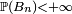
reste vraie, mais n'est pas utile pour démontrer que
propriété vraie, en probabilités, pour toute suite décroissante d'évènements. Par contre la majoration de
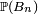
d'une série convergente est toujours indispensable pour conclure que
On termine de la même manière que dans le cas général, à l'aide
pour conclure que