Théorie Dempster-Shafer - Définition

Introduction

La Théorie Dempster-Shafer est une théorie mathématique basée sur la notion de preuves utilisant les fonctions de croyance et le raisonnement plausible. Le but de cette théorie est de permettre de combiner des preuves distinctes pour calculer la probabilité d'un évènement. Cette théorie a été développée par Arthur P. Dempster et Glenn Shafer.

Formalisme mathématique

Soit l’univers, c'est-à-dire l'ensemble contenant tous les éléments. Le power set (ou l'ensemble des parties d'un ensemble), , est l'ensemble de toutes les sous parties de , incluant l'ensemble vide . Par exemple, si:

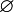
alors

Les éléments du power set peuvent être interprétés comme des propositions, un élément représentant les états qu'il contient. Par exemple, on peut interpréter l'élément comme "la proposition a est vérifiée" ou "on est dans l'état a", ou encore comme "on est soit dans l'état a, soit dans l'état b".

Notion de masse

On définit la masse de la manière suivante :

• la masse de l'ensemble vide est 0 :

• la somme des masses des autres éléments du power set vaut 1 :

La masse d'un élément donné du power set exprime la proportion de toutes les preuves disponibles affirmant que l'état actuel est et pas un autre état ou un sous état de . La valeur de concerne donc seulement l'état et n'apporte aucun crédit aux sous ensembles de , chacun ayant, par définition, sa propre masse.

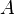
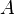
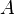
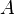
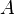
A partir de la valeur de la masse d'un état, on peut définir un intervalle de probabilité. Cet intervalle contient la valeur précise de la probabilité de l'état, et est borné par deux mesures appelées croyance (belief ou support) et plausibilité (plausibility):

La croyance d'un ensemble est définie comme la somme des masses de tous ses sous ensembles (pas nécessairement propres) :

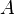
La plausibilité est définie comme la somme des masses de tous les ensembles qui intersectent :

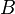
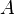
Ces deux mesures sont liées :

De ce fait, la connaissance d'une seule de ces valeurs (masse, croyance ou plausabilité) suffit à déduire les deux autres.

Combinaison de preuves et de masses

Le problème qui se pose maintenant est de savoir comment combiner deux ensembles indépendants et leurs masses. La règle de combinaison originale, connue en tant que Règle de combinaison de Dempster, est une généralisation du théorème de Bayes. Ce théorème met clairement en valeur l'accord entre des sources multiples et ignore les conflits grâce à un facteur de normalisation. L'utilisation de ce théorème pose ainsi problème lorsque des conflits significatifs ont lieu entre différentes sources d'information.

Ici, la combinaison (masse jointe, joint mass) est calculée à partir des deux masses et de la manière suivante :

où

est une mesure du niveau de conflit entre les deux masses. Le facteur de normalisation permet d'ignorer ces conflits et d'attribuer toute masse impliquée dans le conflit à l'ensemble nul. De ce fait, cette opération donne des résultats contre-intuitifs face à des conflits significatifs, dans certains contextes