Théorie de la perturbation de Møller-Plesset - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Méthodes numériques pour le calcul de la structure électronique |
| Hartree-Fock |
| Théorie de la perturbation de Møller-Plesset |
| Interaction de configuration |
| Méthode du cluster couplé |
| Champ multi-configurationnel auto-cohérent |
| Théorie de la perturbation multi-référence |
| Théorie de la fonctionnelle de la densité |
La théorie de la perturbation de Møller-Plesset (MP) est une des nombreuses méthodes post-Hartree-Fock ab initio en chimie quantique appliquée dans le cadre de la chimie numérique. Elle améliore la méthode Hartree-Fock en y apportant les effets de corrélation électronique au moyen de la théorie de la perturbation de Rayleigh-Schrödinger (RS-PT) au deuxième (MP2), troisième (MP3) ou quatrième (MP4) ordre habituellement. L'idée principale de cette méthode a été publiée dès 1934.
Théorie de la perturbation de Rayleigh-Schrödinger
La théorie MP est une application particulière de la théorie de la perturbation de Rayleigh-Schrödinger (en anglais Rayleigh-Schrödinger perturbation theory, RS-PT). Dans la RS-PT, on considère un opérateur hamiltonien non perturbé
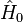
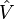
-
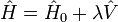
où λ est un paramètre arbitraire réel. Dans la théorie MP, la fonction d'onde d'ordre 0 est une fonction propre exacte de l'opérateur de Fock, qui sert alors d'opérateur non perturbé. La perturbation est le potentiel de corrélation.
Dans la RS-PT, la fonction d'onde perturbée et l'énergie perturbée sont exprimées sous forme de séries entières de λ :
-
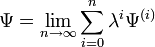
-
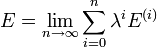
L'inroduction de ces séries dans l'équation de Schrödinger dépendante du temps donne une nouvelle équation :
-
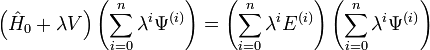
L'égalisation des facteurs des λk dans cette équation donne l'équation de la perturbation d'ordre k, où k=0,1,2, ..., n.
Utilisation des méthodes de perturbation Møller-Plesset
Les calculs Møller-Plesset du second (MP2), du troisième (MP3) et quatrième ordre (MP4) sont les niveaux standard utilisés pour des petits systèmes et sont implémentés dans de nombreux codes de chimie numérique. Des calculs MP de niveau plus élevés, en général seulement du MP5, sont disponibles dans certains codes. Cependant, ils sont rarement utilisés en raison de leurs coûts.
Des études systématiques sur la théorie de la perturbation MP ont montré qu'elle n'est pas forcément convergente à des ordres élevés. Les propriétés de convergence peuvent être lentes, rapides, oscillantes, régulières, hautement erratiques ou simplement inexistantes, selon le système chimique étudié ou la base utilisée. De plus, diverses propriétés moléculaires importantes calculées au niveau MP3 et MP4 ne sont en aucune façon meilleures que leurs équivalents MP2, même pour de petits systèmes. Pour les molécules à couches ouvertes, la théorie MP d'ordre n ne peut être appliquée directement qu'aux fonctions de référence la méthode de Hartree-Fock non restreinte (les états de la méthode Hartree-Fock restreinte ne sont pas des vecteurs propres généraux de l'opérateur de Fock). Cependant, les énergies résultantes « souffrent » d'une sévère contamination de spin, conduisant à des résultats complètement erronés. Une meilleure alternative est d'utiliser une des méthodes similaires à la méthode MP2 basées sur des références Hartree-Fock restreinte pour couche ouverte.
Ces méthodes, Hartree-Fock, Hartree-Fock non-restreinte et Hartree-Fock restreinte utilisent une fonction d'onde à déterminant simple. Les méthodes à champ auto-cohérent multi-configurationnel utilisent plusieurs déterminants et peuvent être utilisées pour l'opérateur non-perturbé, bien qu'il n'y ait pas qu'une seule méthode d'application, comme la théorie de la perturbation de l'espace actif complet (Complete Active Space Perturbation Theory, CASPT2).

















































