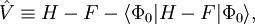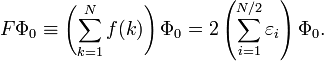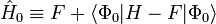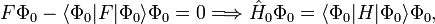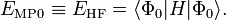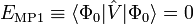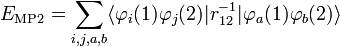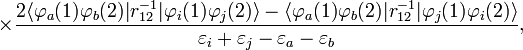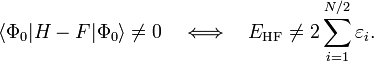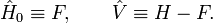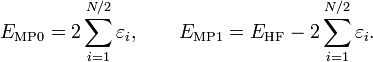Théorie de la perturbation de Møller-Plesset - Définition

Perturbation de Møller-Plesset

Formulation initiale

Les corrections d'énergie MP sont obtenues à partir de la théorie de la perturbation de Rayleigh-Schrödinger (RS) avec la perturbation (potentiel de corrélation) :

dans laquelle le déterminant de Slater normalisé Φ₀ est la fonction propre la plus basse de l'opérateur de Fock :

Ici, N est le nombre d'électrons de la molécule considérée, H est le hamiltonien électrique habituel, f(1) est l'opérateur de Fock mono-électronique, et ε_i est l'énergie orbitalaire appartenant à l'orbitale spatiale doublement occupée φ_i. L'opérateur de Fock décalé

sert d'opérateur non perturbé (ordre zéro).

Le déterminant de Slater Φ₀ étant une fonction propre de F, il s'ensuit que :

donc que l'énergie à l'ordre zéro est la valeur attendue de H en fonction de Φ₀, i.e. l'énergie Hartree-Fock :

Comme l'énergie MP de premier ordre :

est bien sûr nulle, l'énergie de corrélation MP apparait dans le terme de second ordre. Ce résultat est le théorème de Møller-Plesset: « Le potentiel de corrélation ne contribue pas à l'énergie électronique exacte dans le terme de premier ordre ».

Afin d'obtenir la formule MP2 pour une molécule quasiment isolée, la formule de second ordre RS-PT est écrite sur la base de déterminants de Slater doublement excités (les déterminants de Slater mono-excités ne contribuent pas en raison du théorème de Brillouin). Après application des lois de Slater-Condon pour la simplification des éléments de matrices N-électroniques des déterminants de Slater en bra et ket et en intégrant le spin, on obtient :

où phi;_i et φ_j sont les orbitales canoniques occupées et φ_a et φ_b sont les orbitales canoniques virtuelles. Les quantités ε_i, ε_j, ε_a, et ε_b sont les énergies orbitalaires correspondantes. Ainsi, par le terme de second ordre dans le potentiel de corrélation, l'énergie électronique totale est donnée par l'énergie de Hartree-Fock et la correction de second ordre MP : E ≈ E_HF + E_MP2. La solution de l'équation MP à l'ordre zéro (qui par définition est l'équation de Hartree-Fock) donne l'énergie de Hartree-Fock. La première correction de perturbation au-delà du traitement Hartree-Fock qui ne s'annule pas est le terme d'énergie de second ordre.

Formulation alternative

Des expressions équivalentes sont obtenues par une partition légèrement différente du hamiltonien, qui donne une séparation différente des termes d'énergie sur les contributions d'ordre zéro et un, alors qu'à des ordres plus élevés, les deux séparations donnent des résultats identiques. Cette formulation est largement répandue les chimistes, qui sont maintenant de grands utilisateurs de ces méthodes. Cette différence est due au fait, bien connu en théorie Hartree-Fock, que :

(l'énergie Hartree-Fock n'est pas égale à la somme des énergies des orbitales occupées). Dans la séparation alternative, on définit :

On a de manière évidente, dans cette séparation :

Le théorème de Møller-Plesset n'abonde pas dans le sens où E_MP1 ≠ 0. La solution à l'équation MP d'ordre zéro est la somme des énergies orbitalaires. La correction d'ordre zéro plus un donne l'énergie Hartree-Fock. Comme dans la formulation initiale, le premier terme de perturbation qui ne s'annule pas au-delà du traitement Hartree-Fock est l'énergie de second ordre, qui est, rappelons-le, le même dans les deux formulations.