Transmutation de la force - Définition

Démonstration du théorème de transmutation

Cette démonstration peut être soit purement géométrique, soit considérée par l'introduction d'une échelle de temps.

On trouve ici la démonstration géométrique, proposition X des Principia, on reprend le Théorème de Siacci dans le cas de force centrale :

, SH = p longueur de la podaire, R est le rayon de courbure.

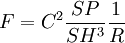
Donc .

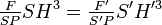
La simple homothétie des triangles S'PH' et SGH donne , d'où :

.

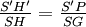
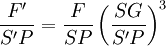
Remarque : on peut préférer la démonstration (directe mais anachronique) du Théorème de Siacci, dans le cas restreint d'un champ central :

Le théorème de Leibniz donne pour le travail élémentaire de la force :

.