Transmutation de la force - Définition

Introduction

Newton , dans les Principia et Calculus, démontre (proposition II, corollaire III) un théorème, appelé par Needham transmutation de la force.

Enoncé : soit un champ central de centre S de force F(r) avec SP = r produisant un mouvement de trajectoire (T), décrit selon la loi des aires (deuxième loi de Kepler).

Alors, cette même trajectoire (T) existe comme solution d'un problème de champ central de centre S' quelconque dans la concavité de (T), de force F'(r'), avec S'P = r', différente évidemment :

.

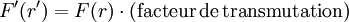
Ce facteur de transmutation vaut : , où SG est le segment parallèle au vecteur , situé entre S et la tangente en P à la trajectoire (T).

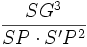
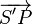
Historiquement, il semblerait que ce soit «la» démonstration de Novembre 1684, réclamée par Halley en Août 1684, celle qui déclencha la rédaction des Principia.

Remarque : il paraît plus simple d'écrire cette loi de transmutation de façon plus symétrique en introduisant et  :

, avec .

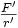
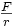
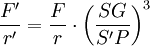
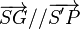
La loi de Hooke se transmute en loi de gravitation

On admet provisoirement le théorème précédent (la démonstration sera faite au prochain paragraphe).

La loi de Hooke a pour équation différentielle :

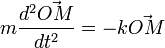
dont solution est :

,

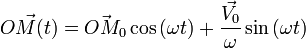
ce qui définit un mouvement elliptique dit de Hooke (de Lissajous, en France), dont le centre de force O est le centre de l'ellipse, décrite périodiquement avec une pulsation .

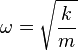
En janvier 1684, Wren défia Hooke, en présence de Halley, de démontrer les lois de Kepler, éventuellement via une loi en . Hooke avait bien tenté de le faire, par un travail semi-empirique (mal connu), qui lui donnait des «elliptoïdes». Mais c'est Newton qui donna la solution en Novembre 1684, après avoir été questionné par Halley en Août 1684.

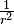
Voici, paraphrasée, sa démonstration, qui utilise le théorème de transmutation.

Soit (T), une trajectoire elliptique de Hooke, de centre O, qui est donc centre de force.

Choisir le foyer S comme nouveau centre de force. Le facteur de transmutation, avec ces nouvelles notations, est .

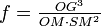
La force devient alors:

.

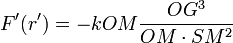
On démontre géométriquement OG = cste = a (demi-grand axe de l'ellipse).

Il vient donc le théorème suivant :

La force de Hooke centrale de centre O, d'expression , est transmutée en la force centrale de centre S, foyer de l'ellipse, d'expression .

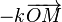
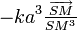
Sous l'action de cette force centrale, la trajectoire (T) est décrite selon la loi des aires de centre S (deuxième loi de Kepler) : on obtient ainsi les deux lois de Kepler. La troisième loi ne présente aucune difficulté particulière, se déduisant aisément de la deuxième loi.

Depuis fort longtemps, on a abandonné cette démonstration, au profit de celle, plus simple, dite de l'hodographe circulaire (d'Hamilton (?) ou de Herman (1710)).

Généralisation selon Goursat

On peut trouver dans Arnold (1990), Needham (1992), et Chandrasekhar (1995), des correspondances entre des champs centraux de lois de puissance différentes.

Soit un champ central en , , et un champ central en ,  : il existe une transmutation qui permet de passer de l'un à l'autre via la formule : (3 − n)(3 − n') = 4.

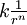
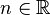
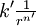
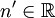
Il est clair que la transmutation d'Arnold est involutive.

On a les cas n = n' = 1 ou n = n' = 5, traités par Newton, puis réutilisés par Maxwell, puis Boltzmann.

Le champ newtonien (n = 2) se transmute en n' = − 1 (Hooke), cas qui vient d'être traité.

Le champ en , donne  : on sait que le cas n = 3 abolit la barrière centrifuge, due à la conservation du moment cinétique ; il est donc normal que n = 3 apparaisse comme cas limite.

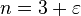
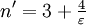
Cette généralisation apparaît déjà dans Goursat.