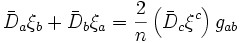Vecteur de Killing conforme - Définition
La liste des auteurs de cet article est disponible ici.
Équation dans une carte locale
Un vecteur de Killing ξ est défini par l'équation
- Daξb + Dbξa = 0,
où D est la dérivation convariante associée à la métrique. Lors d'une transformation conforme, la métrique g est transformée selon
-

où Ω est une fonction ne s'annulant pas. À l'aide de ces définitions, il est possible de calculer l'équivalent de l'équation de Killing à laquelle obéit le vecteur ξ, mais en utilisant la dérivation covariante
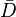

-
où n est la dimension de l'espace considéré.
À partir de la nouvelle métrique
-
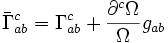
La nouvelle équation de Killing de réécrit donc
-
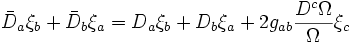
En prenant la trace de cette équation, et en se souvenant que la divergence d'un vecteur de Killing est nulle, il vient
-
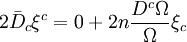
Le membre de droite de la nouvelle équation de Killing peut ainsi être modifié en
-