Aleph-zéro - Définition

Aleph-zero, parfois noté aleph0 ou (?, aleph, étant la première lettre de l'alphabet hébreu), est le cardinal des ensembles infinis dénombrables, comme l'ensemble des entiers naturels .

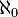
Propriétés

Si l'axiome du choix est utilisé, il est possible de prouver que la classe des nombres cardinaux est totalement ordonnée : est dans ce cas le plus petit nombre cardinal infini.

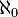
Le cardinal d'un ensemble infini continu, comme l'ensemble des nombres réels , est égal à . Si on accepte l'hypothèse du continu, est égal à (aleph-un).

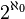
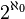
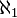
Ensembles infinis dénombrables

Un ensemble infini est dit dénombrable, donc de cardinal , s'il existe une bijection entre lui-même et l'ensemble des entiers naturels.

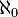
Les ensembles suivants, entre autres, sont de cardinal  :

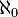
• L'ensemble des entiers naturels
• L'ensemble des entiers relatifs
• L'ensemble des nombres rationnels
• L'ensemble des entiers pairs
• L'ensemble des nombres premiers