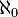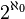Ensemble infini - Définition

En mathématiques, un ensemble est infini s'il n'est pas fini, c'est-à-dire s'il contient un nombre infini d'éléments.
En d'autres termes, si E est un ensemble infini alors  : Le cardinal de E n'est pas un entier naturel. On dit que c'est un nombre transfini.

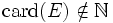
La classe la plus simple des ensembles infinis est la classe des ensembles infinis dits dénombrables (équipotents à ). Une autre classe d'ensembles infinis est la classe des ensembles équipotents à qui sont parfois appelés ensembles continus. Se pose alors le problème de l'hypothèse du continu : existe-t-il un ensemble dont le cardinal est strictement compris entre , qui est le cardinal de et qui est le cardinal de . Cette proposition est indécidable dans le système d'axiomes ZFC.