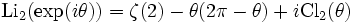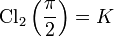Fonction de Clausen - Définition

En mathématiques, la fonction de Clausen est définie par l'intégrale suivante :

Plus généralement, on définit

.

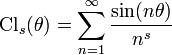
Elle est reliée au polylogarithme par

.

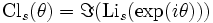
Ernst Kummer et Rogers donnent la relation

valide pour .

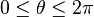
Pour les valeurs rationnelles de (c’est-à-dire, pour pour certains entiers p et q), la fonction peut être comprise comme représentant une orbite périodique d'un élément dans le groupe cyclique, et ainsi peut être exprimé comme une simple somme impliquant la fonction zeta d'Hurwitz.

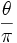
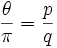
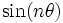
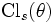
Valeur spéciale

On peut noter l'évaluation suivante :

où K est la constante de Catalan.

Publications en langue anglaise

• Milton Abramowitz and Irene A. Stegun, Handbook of Mathematical Functions, (1964) Dover Publications, New York. ISBN 486-61272-4 . See section 27.8
• Leonard Lewin, (Ed.). Structural Properties of Polylogarithms (1991) American Mathematical Society, Providence, RI. ISBN 0-8218-4532-2