Constante de Catalan - Définition
En mathématiques, la constante de Catalan, nommée d'après le mathématicien Eugène Charles Catalan, est le nombre défini par :
-
-
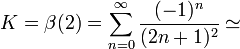
-
où β est la fonction beta de Dirichlet.
On ne sait pas si la constante K est rationnelle ou irrationnelle et on s'attend à ce qu'elle soit transcendante.
Elle est également égale à :
-
-
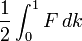
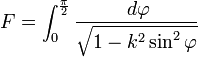
-
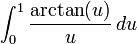
-
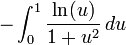
-

-
Bibliographie
- Les nombres remarquables, F. Le Lionnais, Hermann, 1983 puis 1999 (ISBN 2-7056-1407-9)

















































